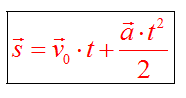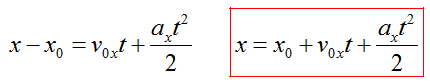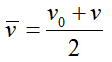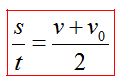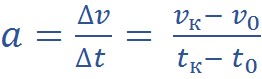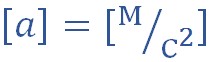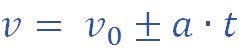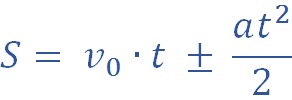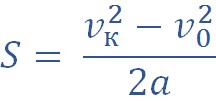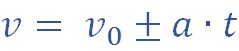I. Механика
Тестирование онлайн
Равноускоренное движение
В этой теме мы рассмотрим очень особенный вид неравномерного движения. Исходя из противопоставления равномерному движению, неравномерное движение — это движение с неодинаковой скоростью, по любой траектории. В чем особенность равноускоренного движения? Это неравномерное движение, но которое «равно ускоряется». Ускорение у нас ассоциируется с увеличением скорости. Вспомним про слово «равно», получим равное увеличение скорости. А как понимать «равное увеличение скорости», как оценить скорость равно увеличивается или нет? Для этого нам потребуется засечь время, оценить скорость через один и тот же интервал времени. Например, машина начинает двигаться, за первые две секунды она развивает скорость до 10 м/с, за следующие две секунды 20 м/с, еще через две секунды она уже двигается со скоростью 30 м/с. Каждые две секунды скорость увеличивается и каждый раз на 10 м/с. Это и есть равноускоренное движение.
Физическая величина, характеризующая то, на сколько каждый раз увеличивается скорость называется ускорением.
Можно ли движение велосипедиста считать равноускоренным, если после остановки в первую минуту его скорость 7км/ч, во вторую — 9км/ч, в третью 12км/ч? Нельзя! Велосипедист ускоряется, но не одинаково, сначала ускорился на 7км/ч (7-0), потом на 2 км/ч (9-7), затем на 3 км/ч (12-9).
Обычно движение с возрастающей по модулю скоростью называют ускоренным движением. Движение же с убывающей скоростью — замедленным движением. Но физики любое движение с изменяющейся скоростью называют ускоренным движением. Трогается ли автомобиль с места (скорость растет!), или тормозит (скорость уменьшается!), в любом случае он движется с ускорением.
Равноускоренное движение — это такое движение тела, при котором его скорость за любые равные промежутки времени изменяется (может увеличиваться или уменьшаться) одинаково
Ускорение тела
Ускорение характеризует быстроту изменения скорости. Это число, на которое изменяется скорость за каждую секунду. Если ускорение тела по модулю велико, это значит, что тело быстро набирает скорость (когда оно разгоняется) или быстро теряет ее (при торможении). Ускорение — это физическая векторная величина, численно равная отношению изменения скорости к промежутку времени, в течение которого это изменение произошло.
Определим ускорение в следующей задаче. В начальный момент времени скорость теплохода была 3 м/с, в конце первой секунды скорость теплохода стала 5 м/с, в конце второй — 7м/с, в конце третьей 9 м/с и т.д. Очевидно, 
. Но как мы определили? Мы рассматриваем разницу скоростей за одну секунду. В первую секунду 5-3=2, во вторую секунду 7-5=2, в третью 9-7=2. А как быть, если скорости даны не за каждую секунду? Такая задача: начальная скорость теплохода 3 м/с, в конце второй секунды — 7 м/с, в конце четвертой 11 м/с.В этом случае необходимо 11-7= 4, затем 4/2=2. Разницу скоростей мы делим на промежуток времени.
Эту формулу чаще всего при решении задач применяют в видоизмененном виде:
Формула записана не в векторном виде, поэтому знак «+» пишем, когда тело ускоряется, знак «-» — когда замедляется.
Направление вектора ускорения
Направление вектора ускорения изображено на рисунках
На этом рисунке машина движется в положительном направлении вдоль оси Ox, вектор скорости всегда совпадает с направлением движения (направлен вправо). Когда вектор ускорение совпадает с направлением скорости, это означает, что машина разгоняется. Ускорение положительное.
При разгоне направление ускорения совпадает с направлением скорости. Ускорение положительное.
На этом рисунке машина движется в положительном направлении по оси Ox, вектор скорости совпадает с направлением движения (направлен вправо), ускорение НЕ совпадает с направлением скорости, это означает, что машина тормозит. Ускорение отрицательное.
При торможении направление ускорения противоположно направлению скорости. Ускорение отрицательное.
Разберемся, почему при торможении ускорение отрицательное. Например, теплоход за первую секунду сбросил скорость с 9м/с до 7м/с, за вторую секунду до 5м/с, за третью до 3м/с. Скорость изменяется на «-2м/с». 3-5=-2; 5-7=-2; 7-9=-2м/с. Вот откуда появляется отрицательное значение ускорения.
При решении задач, если тело замедляется, ускорение в формулы подставляется со знаком «минус».
Перемещение при равноускоренном движении
Дополнительная формула, которую называют безвременной
Формула в координатах
Связь со средней скоростью
При равноускоренном движении среднюю скорость можно рассчитывать как среднеарифметическое начальной и конечной скорости
Из этого правила следует формула, которую очень удобно использовать при решении многих задач
Соотношение путей
Если тело движется равноускоренно, начальная скорость нулевая, то пути, проходимые в последовательные равные промежутки времени, относятся как последовательный ряд нечетных чисел.
Главное запомнить
1) Что такое равноускоренное движение;
2) Что характеризует ускорение;
3) Ускорение — вектор. Если тело разгоняется ускорение положительное, если замедляется — ускорение отрицательное;
3) Направление вектора ускорения;
4) Формулы, единицы измерения в СИ
Упражнения
Два поезда идут навстречу друг другу: один — ускоренно на север, другой — замедленно на юг. Как направлены ускорения поездов?
Одинаково на север. Потому что у первого поезда ускорение совпадает по направлению с движением, а у второго — противоположное движению (он замедляется).
Поезд движется равноускоренно с ускорением a (a>0). Известно, что к концу четвертой секунды скорость поезда равна 6м/с. Что можно сказать о величине пути, пройденном за четвертую секунду? Будет ли этот путь больше, меньше или равен 6м?
Так как поезд движется с ускорением, то скорость его все время возрастает (a>0). Если к концу четвертой секунды скорость равна 6м/с, то в начале четвертой секунды она была меньше 6м/с. Следовательно, путь, пройденный поездом за четвертую секунду, меньше 6м.
Какие из приведенных зависимостей описывают равноускоренное движение? 
Уравнение скорости движущегося тела 
. Каково соответствующее уравнение пути?
*Автомобиль прошел за первую секунду 1м, за вторую секунду 2м, за третью секунду 3м, за четвертую секунду 4м и т.д. Можно ли считать такое движение равноускоренным?
В равноускоренном движении пути, проходимые в последовательные равные промежутки времени, относятся как последовательный ряд нечетных чисел. Следовательно, описанное движение не равноускоренное.
Источник статьи: http://fizmat.by/kursy/kinematika/ravnouskorennoe
Равноускоренное движение
Ускорение – физическая величина, показывающая быстроту изменения скорости. Ускорение равно отношению изменения скорости за промежуток времени к величине этого промежутка
Ускорение – векторная величина, оно имеет направление.
Если вектор ускорения направлен в ту же сторону, что и выбранная нами ось координат, то говорят, что проекция ускорения на ось положительная . Если же ускорение и выбранная ось направлены в разные стороны, то проекция ускорения отрицательная .
Если ускорение и скорость тела направлены в одну сторону, то модуль скорости тела увеличивается, оно разгоняется.
Если ускорение и скорость тела направлены в разные стороны, то модуль скорости тела уменьшается, тело тормозит.
Ускорение в системе СИ измеряется в м/с 2 (метрах, деленных на секунду в квадрате).
Пример. Пусть материальная точка движется вдоль оси ОХ со ускорением a = 2 м/с 2 . Это означает, что за любую секунду движения скорость тела изменяется на 2 м/с.
Равноускоренное прямолинейное движение — движение, при котором ускорение тела остается постоянным (a=const) , а скорость за равные промежутки времени изменяется на одинаковую величину.
Так как ускорение при данном виде движения остается неизменным, то скорость является линейной функцией и вычисляется по формуле:
Перемещение можно рассчитать, применяя следующие формулы:
Обратим внимание, что вторую формулу удобно использовать в задачах, где не дано время движения.
Для прямолинейного равноускоренного движения закон движения выглядит следующим образом:
В записанных уравнениях постановка знаков ± связана со знаками проекций величин скорости, ускорения и перемещения.
Рассмотрим основные графики величин для равноускоренного прямолинейного движения.
Так как модуль ускорения при равноускоренном движении со временем не изменяется, то его график будет представлен в виде прямой линии, параллельной оси времени.
Рис.2.
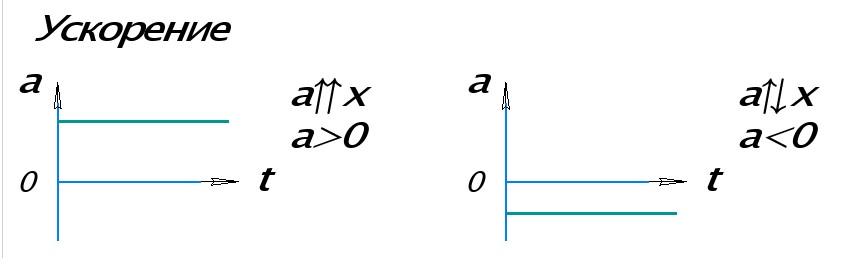
Графики ускорения при равноускоренном прямолинейном движении
На левом рисунке проекция ускорения на ось ОХ, вдоль которой движется тело, положительная. Поэтому график ускорения лежит выше горизонтальной оси t. На правом рисунке ускорение направлено против оси ОХ, его проекция отрицательная. График лежит ниже оси t.
Так как величина скорости тела при данном виде движения рассчитывается по формуле
то ее график будет выглядеть как линейная функция (прямая, расположенная под углом к оси t, исходящая из точки начальной скорости).
На графике слева проекция скорости положительная (υ>0), проекция ускорения тоже положительная (a>0), т.к. скорость тела возрастает со временем. График лежит выше оси t.
На графике справа тело перемещается в направлении, обратном направлению оси ОХ, поэтому проекция скорости отрицательна. Проекция ускорения тоже отрицательна (a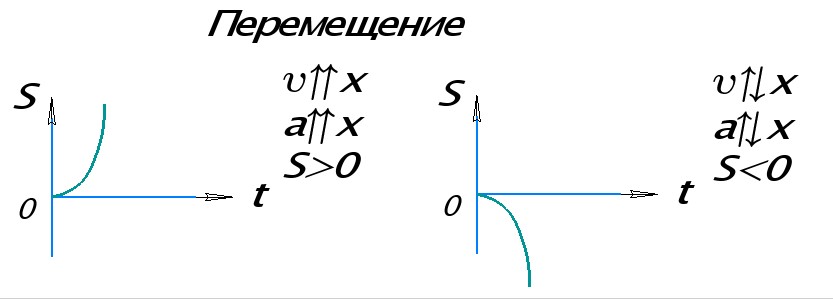 
Рис.4. Графики перемещения при равноускоренном прямолинейном движении
Если ветвь параболы направлена вверх на графике, значит ускорение на этом участке сонаправлено с осью ОХ. Если ветвь параболы направлена вниз, то ускорение направлено против оси ОХ.
График координаты тела представляет собой график перемещения с учетом начальной координаты x0.
Остальные тонкости анализа графиков прямолинейного движения будут рассмотрены в отдельной главе.
Источник статьи: http://www.fizika-express.ru/ravnouskorennoe-dvigeniye/
В помощь школьному учителю физики (урок №1)
«Детей надо учить тому, что пригодится им, когда они вырастут.» Действительно ли эту максиму* высказал Аристипп Киренейский, действительно ли она была произнесена 2400 лет тому назад, следует признать, что это высказывание чертовски верно и актуально во все времена. Детей действительно надо учить тому, что может им пригодиться – и в первую очередь это касается физики. Потому что физика (от греческого φύσις – природа) – это, прежде всего, наука об окружающем нас мире, о том, по каким законам функционирует этот мир. А вовсе не безумные гипотезы вроде Специальной теории относительности, согласно которой 1+1=1 или разнообразные фантазии квантовой физики.
*ПРИМЕЧАНИЕ. Максима – правило поведения или основной принцип, которым люди должны руководствоваться в своих поступках.
На одном из физических форумов кто-то из недалёких граждан (то ли малолетний, то ли великовозрастный), после ознакомления с моей статьёй « Нынешний закон сохранения энергии – величайшее заблуждение современной физики », заявил мне, что «энергия» поступательного движения должна измеряться в кг×м²/с² по той простой причине, что тормозной путь автомобиля пропорционален квадрату его скорости.
Действительно, тормозной путь автомобиля пропорционален квадрату скорости. Но это никоим образом не следует из нынешнего закона сохранения энергии. По той простой причине, что это следует из самого обычного уравнения равноускоренного (равнозамедленного) движения:
Допустим, что после того, как Вы нажали на педаль тормоза, торможение автомобиля происходит равнозамедленно, с каким-то постоянным, равным по величине замедлением (отрицательным ускорением) a . Тогда тормозной путь автомобиля с начала момента торможения составит:
Учитывая, что конечная скорость автомобиля равна 0:
Хочу напомнить, что время торможения будет всегда положительным числом, так как при замедлении движения величина a всегда отрицательная. 🙂
То есть тормозной путь при всех прочих одинаковых параметрах торможения машины действительно пропорционален квадрату начальной скорости, то есть скорости, с которой автомобиль начал торможение. Кому-то может показаться, что расстояние, которое пройдёт автомобиль при торможении, отрицательное, чего быть, в принципе, не может. Величина тормозного пути есть число положительное, так как величина a – замедление, как математическая величина, всегда отрицательная. При этом надо чётко понимать, что никаких отрицательных физических величин в природе, а значит, и в физике, не существует и никогда не существовало.
На практике принято использовать полученное уравнение в виде:
полагая, что на самом деле в уравнении используется не собственно ускорение a , а его модуль | a | . Поэтому более правильной с точки зрения математики была бы запись:
Также сила торможения
где G – вес тела (в нашем случае – автомобиля),
а φ – это коэффициент трения.
Таким образом, согласно классической теории трения, масса автомобиля никак не влияет на длину тормозного пути. А длина тормозного пути определяется прежде всего, скоростью движения, причем зависимость тут – квадратичная. И также определяется коэффициентом (продольного) сцепления, как принято называть φ в среде профессиональных автодорожников и автомобилистов.
При этом действующие ГОСТы иногда дают настолько «профессиональные» и заумные определения, что иногда это определение не понять с первого раза даже нормально образованным людям, победивших в своё время сопромат и теоретическую механику и даже успешно женившихся после этих испытаний. 🙂 Например, читаем ГОСТ 30413-96 «Дороги автомобильные. Метод определения коэффициента сцепления колеса автомобиля с дорожным покрытием»:
3.1 Коэффициент сцепления (продольного) — отношение максимального касательного усилия, действующего вдоль дороги на площади контакта сблокированного колеса с дорожным покрытием, к нормальной реакции в площади контакта колеса с покрытием.)
Хотя, с точки зрения школьной физики φ – это самый что ни на есть обычный коэффициент трения.
Для иллюстрации полученного и осмысления важности этого уравнения
я приведу график и кое-какие высказывания из частично понравившейся мне статьи с сайта autocadabra автора под ник-неймом SaltLake (см. ниже).
Комментируя этот график, SaltLake пишет, цитирую: « Из графика видно, что на скользких поверхностях (лед, снег, мокрый грунт) качество резины не существенно и только трением машину на льду не остановить. Нужно применять другие принципы — протектор, цепляющийся за неровности покрытия, грунтозацепы, цепи или шипы, вгрызающиеся в лед. Участок с коэффициентом трения до 0,8 примерно характеризует поведение обычного автомобиля на асфальте. Для сравнения приведены показатели болида формулы 1. »
Упрощённая таблица величин коэффициентов сцепления приведена ниже. Будущим автомобилистам никогда не стоит забывать, что на мокрой дороге коэффициент сцепления уменьшается примерно вдвое, а на обледенелой дороге падает до катастрофической величины 0,08…0,1.
Я полагаю, что, показывая этот график школьникам, надо заострить их внимание на следующих моментах – что в условиях гололедицы, не столь уж редким явлением на всей территории Российской Федерации, при коэффициенте сцепления 0,08 – 0,10, даже при скорости 60 км/час тормозной путь составит 140 метров, а при скорости 80 км/час – почти 400.
«На практике не существует идеально ровных поверхностей, — пишет SoltLake, — всегда есть неровности, которые цепляются друг за друга. Также не существует идеально чистых поверхностей (металлы всегда покрыты оксидной пленкой, на поверхности находятся грязь и жир). В месте контакта шины с дорогой происходит ее растяжение, деформация и сжатие, из-за чего на некотором участке пятна контакта шина проскальзывает (возникает скольжение). Все это зависит от нагрузки на шину и способность покрышки не подвергаться этим влиянием характеризуется ее индексом нагрузки. Также очень существенно на коэффициент трения влияет температура. Вообще, теория трения — это эмпирическая наука и главным предметом ее изучения является коэффициент трения. Этот коэффициент не является константой и находится в сложной зависимости от очень многих факторов и условий. Их влияния и учет заслуживают отдельного разговора.»
Я настоятельно рекомендую школьным учителям использовать этот материал на уроках физики. Готов выслушать замечания и пожелания.
Источник статьи: http://zen.yandex.ru/media/dpi/v-pomosc-shkolnomu-uchiteliu-fiziki-urok-1-5d2c6df292414d00ad7ec92b