Физика ЕГЭ 2021 ДЕМОВЕРСИЯ Решение задания 5
Физика ЕГЭ 2021 Демоверсия Решение задания 5
5. Автомобиль массой 2 т проезжает верхнюю точку выпуклого моста, двигаясь с постоянной по модулю скоростью 36 км/ч. Радиус кривизны моста равен 40 м.
Из приведённого ниже списка выберите два правильных утверждения, характеризующих движение автомобиля по мосту.
1) Равнодействующая сил, действующих на автомобиль в верхней точке моста, сонаправлена с его скоростью.
2) Сила, с которой мост действует на автомобиль в верхней точке моста, меньше 20 000 Н и направлена вертикально вниз.
3) В верхней точке моста автомобиль действует на мост с силой, равной 15 000 Н.
4) Центростремительное ускорение автомобиля в верхней точке моста равно 2,5 м/с2.
5) Ускорение автомобиля в верхней точке моста направлено противоположно его скорости.
Решение:
Рассмотрим представленную модель. В данном случае движение автомобиля является движением по окружности радиусом R = 40 м.
Центростремительное ускорение при движении по окружности
Сила давления на мост P равна по модулю силе реакции опоры N.
Запишем второй закон Ньютона:
Т.к. вертикально тело не движется (не отрывается от моста), то
Тогда с учетом проекций
1) Нет, т.к. равнодействующая сила равна нулю, она никуда не направлена.
2) Нет, мост действует на автомобиль силой реакции опоры N, она направлена вверх.
3) Да, по расчетам P = 15000 Н.
4) Да, по расчетам = 2,5 м/с 2
5) Нет, в верхней точке присутствует только ускорение , оно направлено в центр окружности, скорость направлена по касательной.
Источник статьи: http://www.fizika-express.ru/fizika-ege-2021-demoversiya-reshenie-zadaniya-5/
Автомобиль выпуклый мост физика
Автомобиль массой 2 т проезжает верхнюю точку выпуклого моста, двигаясь с постоянной по модулю скоростью 36 км/ч. Радиус кривизны моста равен 40 м. Из приведённого ниже списка выберите два правильных утверждения, характеризующих движение автомобиля по мосту.
1) Равнодействующая сил, действующих на автомобиль в верхней точке моста, сонаправлена с его скоростью.
2) Сила, с которой мост действует на автомобиль в верхней точке моста, меньше 20 000 Н и направлена вертикально вниз.
3) В верхней точке моста автомобиль действует на мост с силой, равной 15 000 Н.
4) Центростремительное ускорение автомобиля в верхней точке моста равно 2,5 м/с 2 .
5) Ускорение автомобиля в верхней точке моста направлено противоположно его скорости.
Рассмотрим рисунок, поясняющий движение автомобиля по выпуклому мосту.
1. Неверно. Равнодействующая сил реакции опоры N и силы тяжести mg по второму закону Ньютона сонаправлена с вектором ускорения. А т. к. автомобиль движется по окружности, то ускорение направлено к центру окружности, т. е. вниз. Следовательно, и равнодействующая направлена вниз. Скорость автомобиля при движении по окружности направлена по касательной (в данном случае — горизонтально).
2. Неверно. Сила, с которой мост действует на автомобиль — сила реакции опоры — направлена вертикально вверх.
3. Верно. Сила, с которой автомобиль действует на мост, равна весу тела. По третьему закону Ньютона P = N. Найдём силу реакции опоры по второму закону Ньютона 
Центростремительное ускорение равно 
Значит, Р = 15 кН.
4. Верно. (см. пункт 3).
5. Неверно. Вектор ускорения направлен вертикально вниз, вектор скорости — горизонтально (см. пункт 1).
Источник статьи: http://phys-ege.sdamgia.ru/problem?id=20015
Часть 1. Динамика движения тела по окружности: выпуклый и вогнутый мост, «мертвая петля», конический маятник, тело на вращающемся диске
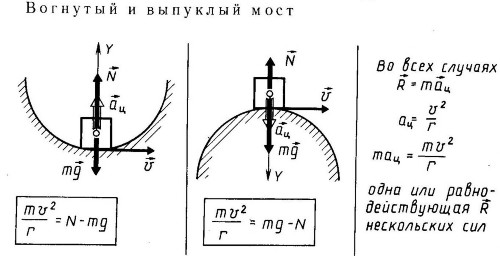
Динамика движения тела по окружности: выпуклый и вогнутый мост, «мертвая петля».
При равномерном движении тела по окружности используется формула ,
,где u- скорость автомобиля; r- радиус кривизны.
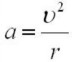
Следует учесть, что в условиях нашего рельефа местности дороги имеют огромное количество подъемов и спусков, поворотов, а это ничто иное, как движение по части окружности.
Автомобиль, движущийся по выпуклому мосту легче того же автомобиля, неподвижно стоящего на том же мосту.
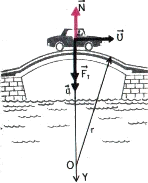
Действительно, движение по выпуклому мосту – это движение по части окружности. Поэтому автомобиль движется с центростремительным ускорением, равным по модулю:
, где u- скорость автомобиля; r- радиус кривизны.
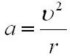
В момент, когда автомобиль находится в высшей точке моста, это ускорение направлено по вертикали вниз. Оно сообщается автомобилю равнодействующей силы тяжести
и силы 
реакции моста.
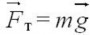
Уравнение, выражающее второй закон Ньютона в векторной форме, запишется так:
Вес автомобиля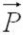 
(сила, с которой он давит на мост) по третьему закону Ньютона направлен противоположно силе реакции моста , а по модулю эти сил равны, следовательно,
Обратите внимание, что при некоторой минимальной скорости
, когда 
автомобиль потеряет опору, а значит и управление, — он взлетает!
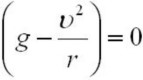
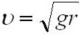
Аналогично можно показать уменьшение веса пассажиров, едущих в автомобиле по выпуклому мосту.
Случай, когда кривизна моста направлена вниз, рассматривается аналогично.
Тогда вес транспортного средства можно найти так:
А еще встречаются случаи:
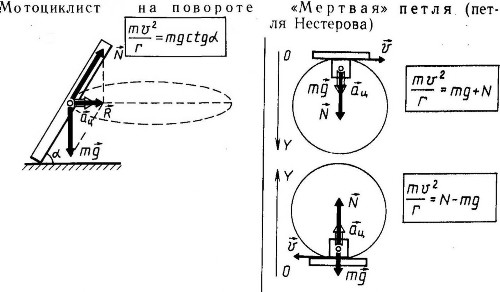
Конический маятник. В коническом маятнике (рис.61) тело маятника (небольшое по размерам тело) вращается в горизонтальной плоскости. Угол, образуемый нитью подвеса с вертикалью, проведенной через точку подвеса, остается неизменным. Вес маятника G можно разложить на две составляющие: центростремительную силу Z, направленную к центру круга, и силу Q, направленную вдоль нити:
Для малых углов конуса h ≈ l; тогда период колебаний конического маятника
Если спроектировать движение конического маятника на вертикальную плоскость, то тень маятника совершает гармоническое движение (рис.62). Закон
гармонического движения легко получить на основе кругового движения (рис. 63):
P = Z cos φ = Z (x : r) = k x, k = Z : r = const.
Гармоническое движение характеризуется тем, что сила, направленная к положению равновесия, пропорциональна удалению маятника от положения равновесия. В процессе колебаний происходит повторяющееся превращение потенциальной энергии в кинетическую и обратно. В точках поворота скорость равна нулю, в положении равновесия скорость максимальна.
Период гармонического колебания:
3. Плоский маятник. Математический маятник.
Колебания маятника, подвешенного на нити (рис.64), при малых углах отклонения ( не превышающих 5º) можно считать гармоническими:
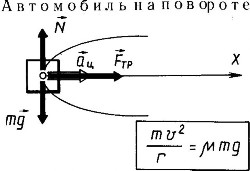
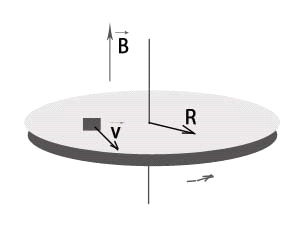
Тело на вращающемся диске.
На расстоянии R от оси горизонтально расположенного диска находится тело, коэффициент трения которого о диск равен k. Диск вращается с угловой скоростью ω.
На тело действуют три силы:
сила тяжести mg, сила реакции опоры N и сила трения Nтр.
В инерциальной системе отсчета, связанной с Землей, второй закон Ньютона будет иметь вид:
Движение тела относительно Земли представляет собой движение в горизонтальной плоскости по окружности радиусом R. Силы, действующие на него в вертикальном направлении, скомпенсированы. Вектор ускорения лежит в горизонтальной плоскости, а само ускорение является центростремительным. Его величина определяется формулой:
Проецирование векторного уравнения на координатные оси X и Y дает два скалярных уравнения:
Первое уравнение показывает, что в роли центростремительной силы выступает сила трения, второе — констатирует, что вертикальные силы взаимно уравновешены.
Сила трения покоя подчиняется неравенству:
поэтому при слишком больших скорости или радиусе вращения сила трения не сможет обеспечить требуемое центростремительное ускорение, и тело начнет соскальзывать.
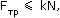
Следовательно, условие отсутствия скольжения:
.
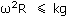
Нам важно ваше мнение! Был ли полезен опубликованный материал? Да | Нет
Источник статьи: http://studopedia.su/16_14583_chast—dinamika-dvizheniya-tela-po-okruzhnosti-vipukliy-i-vognutiy-most-mertvaya-petlya-konicheskiy-mayatnik-telo-na-vrashchayushchemsya-diske.html
Автомобиль выпуклый мост физика
Персональный блог. Темы: физика, ход солнца, солнечные часы
| |
|
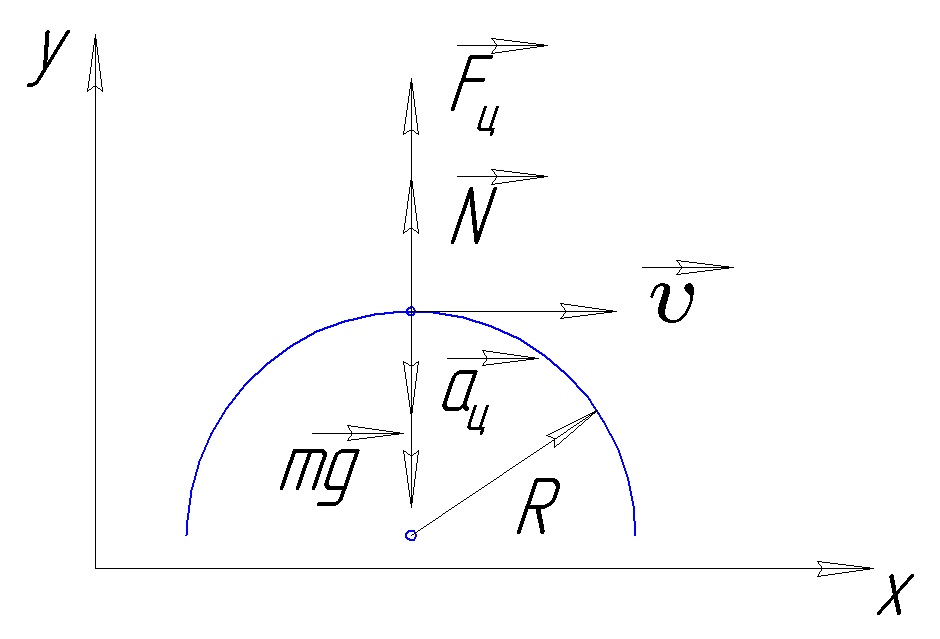
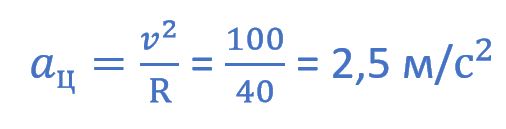
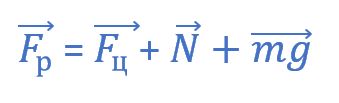
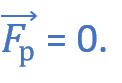
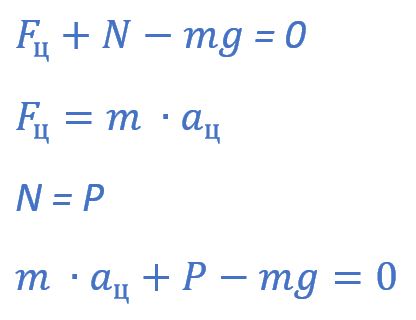
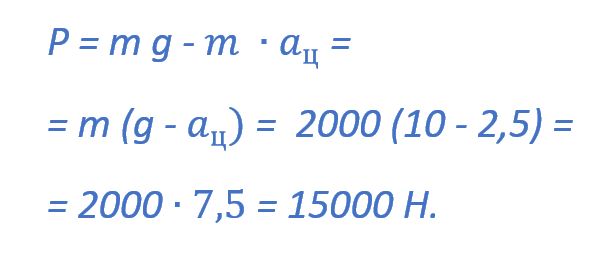
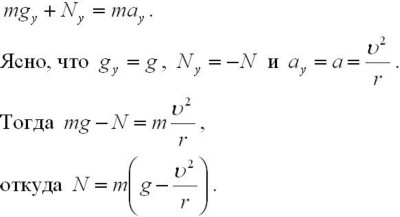
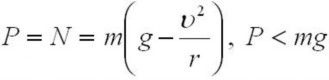
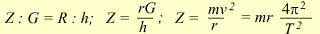
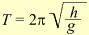
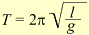
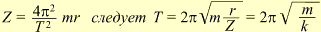
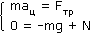
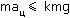
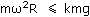
Движение по выпуклому мосту
