До начала торможения автомобиль имел скорость

До начала торможения автомобиль имел скорость

Два автомобиля, выехав одновременно из одного пункта, движутся прямолинейно в одном направлении. Зависимость пройденного ими пути задается уравнениями s₁ = At + Вt 2 и s₂ = Ct + Dt 2 + Ft 3 . Определите относительную скорость автомобилей.

Зависимость скорости тела от времени при прямолинейном движении дана уравнением v = 0,3 t 2 . Найти величину ускорения тела в момент времени 2 с и путь, пройденный телом за интервал времени от 0 до 2 с.

Тело массой m = 4 кг под действием некоторой силы движется прямолинейно согласно уравнению s = Bt+Ct 2 +Dt 3 , где В = 0,5 м/с, С = 3 мс 2 , D = 2 м/с 3 . Определите работу А силы в течение первых двух с половиной секунд.

До начала торможения автомобиль имел скорость v₀ = 60 км/ч. После начала торможения автомобиль двигался прямолинейно с непостоянным ускорением и остановился спустя время t = 3,00 с. За это время он прошел путь s = 20,0 м. Определить среднюю угловую скорость и среднее угловое ускорение колеса автомобиля за время торможения. Радиус колеса R = 0,23 м.

Скорость тела, движущегося прямолинейно, меняется по закону v = A+Bt+Ct 2 , где A = 1 м/с; B = 3 м/с 2 ; C = 6 м/с 3 . Какое расстояние пройдет тело к моменту времени, когда его ускорение станет равным a = 27 м/с 2 ?

Точка движется прямолинейно с ускорением а = 0,2t. Определить момент времени t, когда скорость точки будет равна 2 м/с, если при t₀ = 0 скорость v₀ = 0.

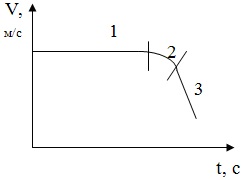
Приведен график зависимости модуля скорости точки, движущейся прямолинейно, от времени. Как изменяется сила, действующая на точку на участках 1, 2, 3? Какой угол она составляет с вектором скорости?

Источник статьи: http://reshenie-zadach.com.ua/fizika/1/dvizhetsya_pryamolinejno.php

До начала торможения автомобиль имел скорость

На последнем километре тормозного пути скорость поезда уменьшилась на 10 м/с. Определите скорость в начале торможения, если общий тормозной путь поезда составил 4 км, а торможение было равнозамедленным. Ответ приведите в м/с.

Определим ускорение, с которым тормозил поезд. Рассмотрим последний километр. Начальная скорость на этом отрезке равна 10 м/с, конечная скорость — 0 м/с. Из формулы сразу находим модуль ускорения Использовав эту же формулу, но теперь уже для всего отрезка торможения, находим начальную скорость:

Тоесть тут подразумевается, что поезд в конечном итоге остановился и не продолжал движение? А то написано, что «На последнем километре тормозного пути скорость поезда уменьшилась на 10 м/с.», что дает повод думать о том, что поезд дальше продолжает движение.

Вроде это стандартная формулировка данной задачи. Тормозной путь — это означает, что не просто уменьшаем скорость, а полностью останавливаемся в конце.

Добрый день! Как вывели формулу для V нулевого?

.

Нигде не могу найти первую формулу. Это вы её как то вывели или она имеется в учебниках? Да и вторую формулу первый раз вижу. под L что подразумевается?

Эта формула, конечно же, должна быть в учебниках. Вот ее вывод, на всякий случай.

Изменение координаты при равноускоренном движении:

.

Зависимость проекции скорости от времени:

.

Из второго равенства, имеем:

.

Подставим это в первую формулу:

.

Здесь — конечная скорость на некотором интервале, а — начальная.

Огромное спасибо. В срочном порядке запишу в шпоры)

Источник статьи: http://phys-ege.sdamgia.ru/problem?id=3437

До начала торможения автомобиль имел скорость

Автомобиль, движущийся в начальный момент времени со скоростью м/с, начал торможение с постоянным ускорением м/с 2 . За – секунд после начала торможения он прошёл путь (м). Определите время, прошедшее от момента начала торможения, если известно, что за это время автомобиль проехал 30 метров. Ответ выразите в секундах.

Найдем, за какое время, прошедшее от момента начала торможения, автомобиль проедет 30 метров:

Значит, через 2 секунды после начала торможения автомобиль проедет 30 метров.

Примечание о выборе корня.

Формула описывает движение автомобиля от начала торможения до полной остановки. Моменту остановки соответствует наибольший пройденный путь. Наибольшее значение квадратного трехчлена достигается в точке в нашем случае Следовательно, через 4 секунды после начала движения автомобиль остановится. Поэтому больший корень уравнения не подходит по смыслу задачи.

Если бы автомобиль после остановки продолжил движение в соответствии с заданной формулой, он поехал бы назад, увеличивая скорость. В некоторый момент времени автомобиль вновь оказался бы на заданном расстоянии от начального положения. Этот момент определяется большим корнем решенного уравнения.

Для читателей, закончивших 9 класс, приведем объяснение в общем виде, опираясь на знания курса физики. При равноускоренном движении Из формулы скорости следует, что при торможении скорость тела достигает нуля в момент времени Поэтому при решении задач на пройденный при торможении путь допустимыми являются моменты времени, не большие t₀.

Рекомендуем сравнить это задание с заданиями 27961 и 27962.

Источник статьи: http://ege.sdamgia.ru/problem?id=27965

В помощь школьному учителю физики (урок №1)

«Детей надо учить тому, что пригодится им, когда они вырастут.» Действительно ли эту максиму* высказал Аристипп Киренейский, действительно ли она была произнесена 2400 лет тому назад, следует признать, что это высказывание чертовски верно и актуально во все времена. Детей действительно надо учить тому, что может им пригодиться – и в первую очередь это касается физики. Потому что физика (от греческого φύσις – природа) – это, прежде всего, наука об окружающем нас мире, о том, по каким законам функционирует этот мир. А вовсе не безумные гипотезы вроде Специальной теории относительности, согласно которой 1+1=1 или разнообразные фантазии квантовой физики.

*ПРИМЕЧАНИЕ. Максима – правило поведения или основной принцип, которым люди должны руководствоваться в своих поступках.

На одном из физических форумов кто-то из недалёких граждан (то ли малолетний, то ли великовозрастный), после ознакомления с моей статьёй « Нынешний закон сохранения энергии – величайшее заблуждение современной физики », заявил мне, что «энергия» поступательного движения должна измеряться в кг×м²/с² по той простой причине, что тормозной путь автомобиля пропорционален квадрату его скорости.

Действительно, тормозной путь автомобиля пропорционален квадрату скорости. Но это никоим образом не следует из нынешнего закона сохранения энергии. По той простой причине, что это следует из самого обычного уравнения равноускоренного (равнозамедленного) движения:

Допустим, что после того, как Вы нажали на педаль тормоза, торможение автомобиля происходит равнозамедленно, с каким-то постоянным, равным по величине замедлением (отрицательным ускорением) a . Тогда тормозной путь автомобиля с начала момента торможения составит:

Учитывая, что конечная скорость автомобиля равна 0:

Хочу напомнить, что время торможения будет всегда положительным числом, так как при замедлении движения величина a всегда отрицательная. 🙂

То есть тормозной путь при всех прочих одинаковых параметрах торможения машины действительно пропорционален квадрату начальной скорости, то есть скорости, с которой автомобиль начал торможение. Кому-то может показаться, что расстояние, которое пройдёт автомобиль при торможении, отрицательное, чего быть, в принципе, не может. Величина тормозного пути есть число положительное, так как величина a – замедление, как математическая величина, всегда отрицательная. При этом надо чётко понимать, что никаких отрицательных физических величин в природе, а значит, и в физике, не существует и никогда не существовало.

На практике принято использовать полученное уравнение в виде:

полагая, что на самом деле в уравнении используется не собственно ускорение a , а его модуль | a | . Поэтому более правильной с точки зрения математики была бы запись:

Также сила торможения

где G – вес тела (в нашем случае – автомобиля),

а φ – это коэффициент трения.

Таким образом, согласно классической теории трения, масса автомобиля никак не влияет на длину тормозного пути. А длина тормозного пути определяется прежде всего, скоростью движения, причем зависимость тут – квадратичная. И также определяется коэффициентом (продольного) сцепления, как принято называть φ в среде профессиональных автодорожников и автомобилистов.

При этом действующие ГОСТы иногда дают настолько «профессиональные» и заумные определения, что иногда это определение не понять с первого раза даже нормально образованным людям, победивших в своё время сопромат и теоретическую механику и даже успешно женившихся после этих испытаний. 🙂 Например, читаем ГОСТ 30413-96 «Дороги автомобильные. Метод определения коэффициента сцепления колеса автомобиля с дорожным покрытием»:

3.1 Коэффициент сцепления (продольного) — отношение максимального касательного усилия, действующего вдоль дороги на площади контакта сблокированного колеса с дорожным покрытием, к нормальной реакции в площади контакта колеса с покрытием.)

Хотя, с точки зрения школьной физики φ – это самый что ни на есть обычный коэффициент трения.

Для иллюстрации полученного и осмысления важности этого уравнения

я приведу график и кое-какие высказывания из частично понравившейся мне статьи с сайта autocadabra автора под ник-неймом SaltLake (см. ниже).

Комментируя этот график, SaltLake пишет, цитирую: « Из графика видно, что на скользких поверхностях (лед, снег, мокрый грунт) качество резины не существенно и только трением машину на льду не остановить. Нужно применять другие принципы — протектор, цепляющийся за неровности покрытия, грунтозацепы, цепи или шипы, вгрызающиеся в лед. Участок с коэффициентом трения до 0,8 примерно характеризует поведение обычного автомобиля на асфальте. Для сравнения приведены показатели болида формулы 1. »

Упрощённая таблица величин коэффициентов сцепления приведена ниже. Будущим автомобилистам никогда не стоит забывать, что на мокрой дороге коэффициент сцепления уменьшается примерно вдвое, а на обледенелой дороге падает до катастрофической величины 0,08…0,1.

Я полагаю, что, показывая этот график школьникам, надо заострить их внимание на следующих моментах – что в условиях гололедицы, не столь уж редким явлением на всей территории Российской Федерации, при коэффициенте сцепления 0,08 – 0,10, даже при скорости 60 км/час тормозной путь составит 140 метров, а при скорости 80 км/час – почти 400.

«На практике не существует идеально ровных поверхностей, — пишет SoltLake, — всегда есть неровности, которые цепляются друг за друга. Также не существует идеально чистых поверхностей (металлы всегда покрыты оксидной пленкой, на поверхности находятся грязь и жир). В месте контакта шины с дорогой происходит ее растяжение, деформация и сжатие, из-за чего на некотором участке пятна контакта шина проскальзывает (возникает скольжение). Все это зависит от нагрузки на шину и способность покрышки не подвергаться этим влиянием характеризуется ее индексом нагрузки. Также очень существенно на коэффициент трения влияет температура. Вообще, теория трения — это эмпирическая наука и главным предметом ее изучения является коэффициент трения. Этот коэффициент не является константой и находится в сложной зависимости от очень многих факторов и условий. Их влияния и учет заслуживают отдельного разговора.»

Я настоятельно рекомендую школьным учителям использовать этот материал на уроках физики. Готов выслушать замечания и пожелания.

Источник статьи: http://zen.yandex.ru/media/dpi/v-pomosc-shkolnomu-uchiteliu-fiziki-urok-1-5d2c6df292414d00ad7ec92b

В помощь школьному учителю физики (урок №1)

«Детей надо учить тому, что пригодится им, когда они вырастут.» Действительно ли эту максиму* высказал Аристипп Киренейский, действительно ли она была произнесена 2400 лет тому назад, следует признать, что это высказывание чертовски верно и актуально во все времена. Детей действительно надо учить тому, что может им пригодиться – и в первую очередь это касается физики. Потому что физика (от греческого φύσις – природа) – это, прежде всего, наука об окружающем нас мире, о том, по каким законам функционирует этот мир. А вовсе не безумные гипотезы вроде Специальной теории относительности, согласно которой 1+1=1 или разнообразные фантазии квантовой физики.

*ПРИМЕЧАНИЕ. Максима – правило поведения или основной принцип, которым люди должны руководствоваться в своих поступках.

На одном из физических форумов кто-то из недалёких граждан (то ли малолетний, то ли великовозрастный), после ознакомления с моей статьёй « Нынешний закон сохранения энергии – величайшее заблуждение современной физики », заявил мне, что «энергия» поступательного движения должна измеряться в кг×м²/с² по той простой причине, что тормозной путь автомобиля пропорционален квадрату его скорости.

Действительно, тормозной путь автомобиля пропорционален квадрату скорости. Но это никоим образом не следует из нынешнего закона сохранения энергии. По той простой причине, что это следует из самого обычного уравнения равноускоренного (равнозамедленного) движения:

Допустим, что после того, как Вы нажали на педаль тормоза, торможение автомобиля происходит равнозамедленно, с каким-то постоянным, равным по величине замедлением (отрицательным ускорением) a . Тогда тормозной путь автомобиля с начала момента торможения составит:

Учитывая, что конечная скорость автомобиля равна 0:

Хочу напомнить, что время торможения будет всегда положительным числом, так как при замедлении движения величина a всегда отрицательная. 🙂

То есть тормозной путь при всех прочих одинаковых параметрах торможения машины действительно пропорционален квадрату начальной скорости, то есть скорости, с которой автомобиль начал торможение. Кому-то может показаться, что расстояние, которое пройдёт автомобиль при торможении, отрицательное, чего быть, в принципе, не может. Величина тормозного пути есть число положительное, так как величина a – замедление, как математическая величина, всегда отрицательная. При этом надо чётко понимать, что никаких отрицательных физических величин в природе, а значит, и в физике, не существует и никогда не существовало.

На практике принято использовать полученное уравнение в виде:

полагая, что на самом деле в уравнении используется не собственно ускорение a , а его модуль | a | . Поэтому более правильной с точки зрения математики была бы запись:

Также сила торможения

где G – вес тела (в нашем случае – автомобиля),

а φ – это коэффициент трения.

Таким образом, согласно классической теории трения, масса автомобиля никак не влияет на длину тормозного пути. А длина тормозного пути определяется прежде всего, скоростью движения, причем зависимость тут – квадратичная. И также определяется коэффициентом (продольного) сцепления, как принято называть φ в среде профессиональных автодорожников и автомобилистов.

При этом действующие ГОСТы иногда дают настолько «профессиональные» и заумные определения, что иногда это определение не понять с первого раза даже нормально образованным людям, победивших в своё время сопромат и теоретическую механику и даже успешно женившихся после этих испытаний. 🙂 Например, читаем ГОСТ 30413-96 «Дороги автомобильные. Метод определения коэффициента сцепления колеса автомобиля с дорожным покрытием»:

3.1 Коэффициент сцепления (продольного) — отношение максимального касательного усилия, действующего вдоль дороги на площади контакта сблокированного колеса с дорожным покрытием, к нормальной реакции в площади контакта колеса с покрытием.)

Хотя, с точки зрения школьной физики φ – это самый что ни на есть обычный коэффициент трения.

Для иллюстрации полученного и осмысления важности этого уравнения

я приведу график и кое-какие высказывания из частично понравившейся мне статьи с сайта autocadabra автора под ник-неймом SaltLake (см. ниже).

Комментируя этот график, SaltLake пишет, цитирую: « Из графика видно, что на скользких поверхностях (лед, снег, мокрый грунт) качество резины не существенно и только трением машину на льду не остановить. Нужно применять другие принципы — протектор, цепляющийся за неровности покрытия, грунтозацепы, цепи или шипы, вгрызающиеся в лед. Участок с коэффициентом трения до 0,8 примерно характеризует поведение обычного автомобиля на асфальте. Для сравнения приведены показатели болида формулы 1. »

Упрощённая таблица величин коэффициентов сцепления приведена ниже. Будущим автомобилистам никогда не стоит забывать, что на мокрой дороге коэффициент сцепления уменьшается примерно вдвое, а на обледенелой дороге падает до катастрофической величины 0,08…0,1.

Я полагаю, что, показывая этот график школьникам, надо заострить их внимание на следующих моментах – что в условиях гололедицы, не столь уж редким явлением на всей территории Российской Федерации, при коэффициенте сцепления 0,08 – 0,10, даже при скорости 60 км/час тормозной путь составит 140 метров, а при скорости 80 км/час – почти 400.

«На практике не существует идеально ровных поверхностей, — пишет SoltLake, — всегда есть неровности, которые цепляются друг за друга. Также не существует идеально чистых поверхностей (металлы всегда покрыты оксидной пленкой, на поверхности находятся грязь и жир). В месте контакта шины с дорогой происходит ее растяжение, деформация и сжатие, из-за чего на некотором участке пятна контакта шина проскальзывает (возникает скольжение). Все это зависит от нагрузки на шину и способность покрышки не подвергаться этим влиянием характеризуется ее индексом нагрузки. Также очень существенно на коэффициент трения влияет температура. Вообще, теория трения — это эмпирическая наука и главным предметом ее изучения является коэффициент трения. Этот коэффициент не является константой и находится в сложной зависимости от очень многих факторов и условий. Их влияния и учет заслуживают отдельного разговора.»

Я настоятельно рекомендую школьным учителям использовать этот материал на уроках физики. Готов выслушать замечания и пожелания.

Источник статьи: http://zen.yandex.ru/media/dpi/v-pomosc-shkolnomu-uchiteliu-fiziki-urok-1-5d2c6df292414d00ad7ec92b