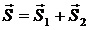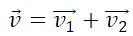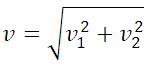ИНФОФИЗ — мой мир.
Весь мир в твоих руках — все будет так, как ты захочешь
Весь мир в твоих руках — все будет так, как ты захочешь
Как сказал.
Если вы студент, значит перед вами стоит тысяча возможностей. Найдите в себе силы, чтобы использовать хотя бы одну из них.
Тестирование
Урок 02. (дополнительный материал). Относительность механического движения
Относительность механического движения.
Механическое движение относительно. Движение одного и того же тела относительно разных тел оказывается различным.
Например, автомобиль движется по дороге. В автомобиле находятся люди. Люди движутся вместе с автомобилем по дороге. То есть люди перемещаются в пространстве относительно дороги. Но относительно самого автомобиля люди не движутся. В этом проявляетсяотносительность механического движения.
Для описания движения тела нужно указать, по отношению к какому телу рассматривается движение. Это тело называют телом отсчета. Покой тоже относителен. Например, пассажир в покоящемся поезде смотрит на проходящий мимо поезд и не понимает, какой поезд движется, пока не посмотрит на небо или землю.
Все тела во Вселенной движутся, поэтому не существует тел, которые находятся в абсолютном покое. По той же причине определить движется тело или нет, можно только относительно какого-либо другого тела.
Например, автомобиль движется по дороге. Дорога находится на планете Земля. Дорога неподвижна. Поэтому можно измерить скорость автомобиля относительно неподвижной дороги. Но дорога неподвижна относительно Земли. Однако сама Земля вращается вокруг Солнца. Следовательно, дорога вместе с автомобилем также вращается вокруг Солнца. Следовательно, автомобиль совершает не только поступательное движение, но и вращательное (относительно Солнца). А вот относительно Земли автомобиль совершает только поступательное движение. В этом проявляется относительность механического движения.
Движение одного и того же тела может выглядеть по-разному с точки зрения различных наблюдателей. Скорость, направление движения и вид траектории тела будут различными для различных наблюдателей. Без указания тела отсчета разговор о движении является бессмысленным. Например, сидящий пассажир в поезде покоится относительно вагона, но движется вместе с вагоном относительно платформы вокзала.
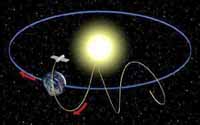
Проиллюстрируем теперь для различных наблюдателей различие вида траектории движущегося тела. Находясь на Земле, на ночном небе легко можно видеть яркие быстро летящие точки — спутники. Они движутся по круговым орбитам вокруг Земли, то есть вокруг нас. Сядем теперь в космический корабль, летящий к Солнцу. Мы увидим, что теперь каждый спутник движется не по окружности вокруг Земли, а по спирали вокруг Солнца:
Относительность механического движения – это зависимость траектории движения тела, пройденного пути, перемещения и скорости от выбора системы отсчёта.
Движение тел можно описывать в различных системах отсчета. С точки зрения кинематики все системы отсчета равноправны. Однако кинематические характеристики движения, такие как траектория, перемещение, скорость, в разных системах оказываются различными. Величины, зависящие от выбора системы отсчета, в которой производится их измерение, называют относительными.
Галилей показал, что в условиях Земли практически справедлив закон инерции. Согласно этому закону действие на тело сил проявляется в изменениях скорости; для поддержания же движения с неизменной по величине и направлению скоростью не требуется присутствия сил. Системы отсчета, в которых выполняется закон инерции, стали называть инерциальные системы отсчета (ИСО).
Системы, которые вращаются или ускоряются, неинерциальные.
Землю нельзя считать вполне ИСО: она вращается, но для большинства наших целей системы отсчета, связанные с Землей, в достаточно хорошем приближении можно принять за инерциальные. Система отсчета, движущаяся равномерно и прямолинейно относительно ИСО, также инерциальная.
Г. Галилей и И. Ньютон глубоко осознавали то, что мы сегодня называем принципом относительности, согласно которому механические законы физики должны быть одинаковыми во всех ИСО при одинаковых начальных условиях.
Из этого следует: ни одна ИСО ничем не отличается от другой системы отсчета. Все ИСО эквивалентны с точки зрения механических явлений.
Принцип относительности Галилея исходит из некоторых допущений, которые опираются на наш повседневный опыт. В классической механике пространство и время считаются абсолютными. Предполагается, что длина тел одинакова в любой системе отсчета и что время в различных системах отсчета течет одинаково. Предполагается, что масса тела, а также все силы остаются неизменными при переходе из одной ИСО в другую.
В справедливости принципа относительности нас убеждает повседневный опыт, например в равномерно движущемся поезде или самолете тела движутся так же, как и на Земле.
Не существует эксперимента, с помощью которого можно было бы установить, какая система отсчета действительно покоится, а какая движется. Нет систем отсчета в состоянии абсолютного покоя.
Если на движущейся тележке подбросить монету вертикально вверх, то в системе отсчета, связанной с тележкой, будет изменяться только координата ОУ.
В системе отсчета, связанной с Землей, изменяются координаты ОУ и ОХ.
Следовательно, положение тел и их скорости в разных системах отсчета различны.
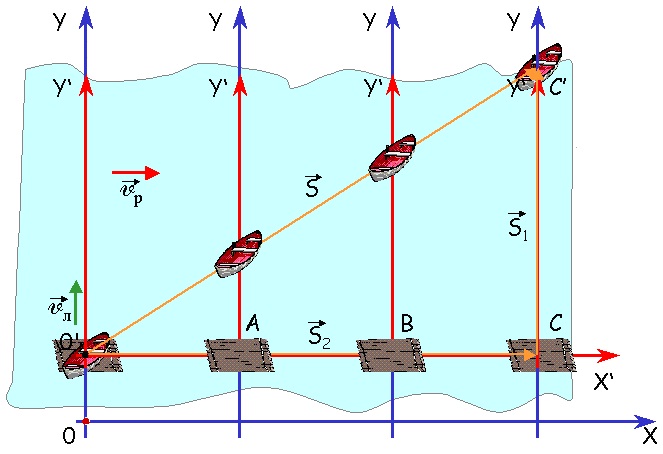
Рассмотрим движение одного и того же тела относительно двух разных систем отсчета: неподвижной и движущейся.
Лодка пересекает реку перпендикулярно течению реки двигаясь с некоторой скоростью относительно воды. За движением лодки следят 2 наблюдателя: один неподвижный на берегу, другой на плоту, плывущем по течению. Относительно воды плот неподвижен, а по отношению к берегу он движется со скоростью течения.
С каждым наблюдателем свяжем систему координат.
X0Y – неподвижная система координат.
X’0’Y’ – подвижная система координат.
S – перемещение лодки относительно неподвижной СО.
S1 – перемещение лодки относительно подвижной СО
S2 – перемещение подвижной системы отсчета относительно неподвижной СО.
По закону сложения векторов 
Скорость получим разделив S на t: 
v – скорость тела относительно неподвижной СО
v1 – скорость тела относительно подвижной СО
v2 – скорость подвижной системы отсчета относительно неподвижной СО
Эта формула выражает классический закон сложения скоростей: скорость тела относительно неподвижной СО равна геометрической сумме скорости тела относительно подвижной СО и скорости подвижной СО относительно неподвижной СО.
В скалярном виде формула будет иметь вид: 
Впервые эту формулу получил Галилей.
Принцип относительности Галилея: все инерциальные системы отсчета равноправны; ход времени, масса, ускорение и сила в них записываются одинаково.
Скачать презентацию с Яндекса
Источник статьи: http://infofiz.ru/index.php/mirfiziki/fizst/lkf/4-lk2md
Относительное движение
Скорость точки относительно неподвижной системы отсчета равна векторной сумме скорости движущейся системы и скорости точки относительно движущейся системы.
\(v\) — абсолютная скорость
\(\vec\) — переносная скорость
\(v’\) — относительная скорость
Дятел стучит по дереву, делая 30 ударов в минуту, а мальчик, который едет в автомобиле слышит 31 удар в минуту. Найдите скорость автомобиля, если скорость звука 330 м/с.
Дятел делает 0,5 ударов в секунду. Для того, чтобы мальчик услышал 31 удар , нужно чтобы звук прошел за две секунды на \(330\text < м/с>\cdot 2\text < с>\) меньше. Значит скорость автомобиля будет \[v_1=\dfrac <330\text< м/с>\cdot 2\text< с>><60\text< с>>=11\text< м/с>\]
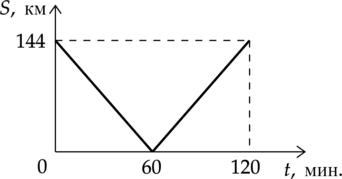
Из двух городов навстречу друг другу с постоянной скоростью движутся два автомобиля. На графике показано изменение расстояния между автомобилями с течением времени. Каков модуль скорости первого автомобиля в системе отсчёта, связанной со вторым автомобилем?
За 60 минут расстояние между автомобилями изменилось с 144 км до 0 км, то есть автомобили встретились. Вычислим скорость первого автомобиля в системе отсчёта, связанной со вторым автомобилем: \[v=\dfrac<144000\text< м>><3600\text< с>>=40\text< м/с>\]
Автобус везёт пассажиров по прямой дороге со скоростью 10 м/с. Пассажир равномерно идёт по салону автобуса со скоростью 1 м/с относительно автобуса, двигаясь от задней двери к кабине водителя. Чему равен модуль скорости пассажира относительно дороги? (Ответ дайте в метрах в секунду.)
Так как пассажир идет в том же направлении, что и автобус, то вектора их скоростей складываются, поэтому абсолютная скорость равна \[\upsilon_<\text<абс>>=\upsilon_<\text<пер>>+\upsilon_<\text<отн>>=10\text< м/с>+1\text< м/с>=11\text< м/с>\]
По прямой дороге с постоянной скоростью 100 км/ч едет мотоциклист и в том же направлении едет автомобиль с постоянной скоростью 70 км/ч. Чему равен модуль скорости движения мотоцикла относительно автомобиля? (Ответ дайте в километрах в час.)
Катер плывёт по прямой реке, двигаясь относительно берега перпендикулярно береговой линии. Модуль скорости катера относительно берега равен 8 км/ч. Река течёт со скоростью 6 км/ч. Чему равен модуль скорости катера относительно воды? Ответ выразите в км/ч.
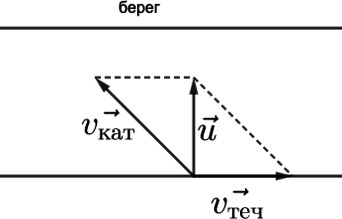
Чтобы катер двигался перпендикулярно относительно берега, относительно воды ему надо двигаться под углом. По закону сложения скоростей: \[\vec
По теореме Пифагора найдем скорость катера относительно воды: \[v_<\text<кат>>=\sqrt
Пассажир зашел в автобус через заднюю дверь. Автобус поехал с постоянной скоростью \(\upsilon_1=25\) м/с, а пассажир пошел к передней части автобуса. Скорость пассажира относительно автобуса равна \(\upsilon_<2>=3\) м/с. С какой скоростью едет автобус относительно пассажира?
Скорость первого тела относительного второго равна скорости второго тела относительно первого и направлена в противоположную сторону. \[\vec
Вася идет по прямой дороге со скоростью \(\upsilon_1=3\text< км/ч>.\) Навстречу ему движется грузовик со скоростью \(\upsilon_2=30\text< км/ч>\) . С какой скоростью \(\upsilon_3\) (по модулю) должен двигаться велосипедист навстречу Васе, чтобы модули его скорости относительно автомобиля и относительно Васи были одинаковы? Ответ дайте в км/ч.
По закону сложения скоростей относительно автомобиля: \[\vec<\upsilon>_3=\vec<\upsilon>_2+\vec<\upsilon>_<32>,\] \[Ox: \upsilon_3=\upsilon_2+\upsilon_<32>,\] где в данном случае \(\upsilon_2\) — скорость системы отсчета, а \(\upsilon_<32>\) — скорость велосипедиста относительно автомобиля. Выразим \(\upsilon_<32>\) : \[\upsilon_<32>=\upsilon_<3>-\upsilon_<2>\] \(\upsilon_ <3>(автомобиль явно быстрее велосипеда), значит: \[|\upsilon_<32>|=|\upsilon_<3>-\upsilon_<2>|=\upsilon_<2>-\upsilon_<3>\quad(1)\] По закону сложения скоростей относительно Васи (Учитывая, что велосипедист двигается в противоположном направлении от Васи): \[\vec<\upsilon>_<3>=\vec<\upsilon>_<1>+\vec<\upsilon>_<23>,\] \[Ox: \upsilon_<3>=-\upsilon_<1>+\upsilon_<23>,\] где в данном случае \(\upsilon_<1>\) — скорость системы отсчета, а \(\upsilon_<23>\) — скорость велосипедиста относительно Васи. Выразим \(\upsilon_<23>\) : \[\upsilon_<23>=\upsilon_<1>+\upsilon_<3>\quad(2)\] По условию: \[|\upsilon_<32>|=|\upsilon_<23>|\] Подсавив сюда \((1)\) и \((2)\) , получим: \[\upsilon_<2>-\upsilon_<3>=\upsilon_<1>+\upsilon_<3>\] Выразим \(\upsilon_3\) : \[\upsilon_3=\dfrac<\upsilon_2-\upsilon_1><2>=\dfrac<30\text< км/ч>-3\text< км/ч>><2>=13,5\text< км/ч>\]
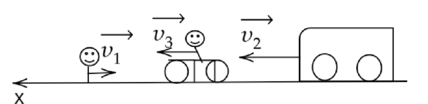
Источник статьи: http://physics.shkolkovo.net/catalog/kinematika/otnositelnoe-dvizhenie
Учебники
Журнал «Квант»
Общие
Уровень B
1. Приведите примеры относительно каких тел покоится плот, плывущий по течению? Относительно каких тел движется?
2. Может ли человек, находясь на движущемся эскалаторе метро, быть в покое в системе отсчета, связанной с землей?
3. Почему нельзя применять паруса для управления полетом воздушного шара?
4. Туристы плывут на плоту по реке, и один из них плавает вокруг плота. Изобразите траекторию движения пловца относительно:
а) наблюдателя на плоту,
б) наблюдателя, который находится на высоком обрыве около реки.
5. Изобразите траекторию движения точки обода велосипедного колеса при прямолинейном движении велосипеда по дороге в системах отсчета, жестко связанных:
а) с велосипедистом;
б) с наблюдателем, стоящим сбоку.
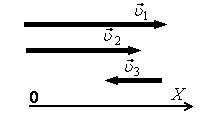
6. На рисунке 1 даны направления движения трех тел. Модули их скоростей относительно неподвижного наблюдателя соответственно равны: υ1 = 5 м/с, υ2 = 4 м/с, υ3 = 2 м/с. Применяя закон сложения скоростей, определите скорости движения тел относительно:
б) третьего тела.
Соответствует ли полученный ответ вашей интуиции?
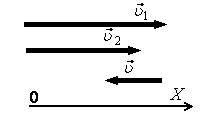
7. На рисунке 2 даны направления движения трех тел. Модули скоростей первого и второго тела относительно неподвижного наблюдателя соответственно равны: υ1 = 5 м/с, υ2 = 4 м/с. Скорость третьего тела относительно второго по модулю равна υ3 = 3 м/с. Определите скорость третьего тела относительно:
а) неподвижного наблюдателя;
8. Скорость пловца относительно воды 1,2 м/с. Скорость течения 0,8 м/с. Определите скорость пловца относительно берега, если пловец плывет по течению реки.
9. Скорость велосипедиста 36 км/ч, а скорость встречного ветра 4 м/с. Какова скорость ветра в системе отсчета, связанной с велосипедистом?
10. Определите скорость ветра, если двигатель самолета сообщает ему в безветренную погоду скорость равную 900 км/ч, а при встречном ветре 850 км/ч.
11. По дороге движутся автомобиль со скоростью 15 м/с и велосипедист со скоростью 5 м/с. Определите скорость их сближения, если:
а) автомобиль догоняет велосипедиста;
б) они движутся навстречу друг другу.
12. Эскалатор метро движется со скоростью 0,75 м/с. Найдите время, за которое пассажир переместится на 20 м относительно земли, если он сам идет в направлении движения эскалатора со скоростью 0,25 м/с в системе отсчета, связанной с эскалатором.
13. Два автомобиля движутся навстречу друг другу с равными скоростями по 80 км/ч каждая. За какое время расстояние между ними уменьшится на 10 км?
14. По двум параллельным железнодорожным линиям равномерно движутся два поезда: грузовой длиной 630 м со скоростью 48 км/ч и пассажирский длиной 120 м со скоростью 102 км/ч. В течение какого времени пассажирский поезд проходит мимо машиниста грузового, если поезда движутся:
а) в одном направлении;
б) навстречу друг другу?
15. Пассажир, сидящий у окна поезда, идущего со скоростью 72 км/ч, видит в течение 10 с встречный поезд. Длина встречного поезда 290 м. Определите его скорость.
16. Скорость течения 3 м/с, а рыбак может грести со скоростью 5 м/с при неподвижной воде. Определите время, необходимое рыбаку, чтобы спуститься на 40 м вниз по течению и на столько же подняться вверх.
Уровень C
1. Скорость движения теплохода относительно берега вниз по реке 20 км/ч, а вверх – 18 км/ч. Определите скорость течения относительно берега и скорость теплохода относительно воды.
2. Автоколонна длиной 1,2 км движется со скоростью 36 км/ч. Мотоциклист выезжает из головы колонны, доезжает до ее хвоста и возвращается обратно. Определите время, за которое мотоциклист преодолеет данное расстояние, если его скорость равна 72 км/ч.
3. Пловец, двигаясь относительно воды перпендикулярно течению со скоростью 5 км/ч, переплывает реку шириной 120 м. Скорость течения 3,24 км/ч. Определите:
а) скорость пловца относительно берега;
б) время, которое требуется пловцу, чтобы переплыть реку;
в) перемещение пловца относительно берега;
г) под каким углом к берегу плывет пловец?
4. Вертолет летел в безветренную погоду на север со скоростью 20 м/с. С какой скоростью и под каким углом к первоначальному направлению будет лететь вертолет, если подует западный ветер со скоростью 10 м/с?
5. На катере необходимо переплыть реку перпендикулярно берега. Какую скорость должен сообщить мотор катеру, чтобы при скорости течения реки, равной 1,2 м/с, катер двигался относительно берега со скоростью 3,2 м/с?
6. Пловец желает переплыть реку перпендикулярно берега. Под каким углом к течению он должен плыть, если скорость пловца относительно воды 1 м/с, скорость течения 0,8 м/с?
7. Скорость течения реки 4 км/ч, ширина ее 240 м. С какой скоростью относительно берега должен плыть пловец, чтобы переплыть реку за 15 мин, если его скорость относительно воды перпендикулярна берегу?
8. По двум взаимно перпендикулярным дорогам движутся равномерно грузовая и легковая машины со скоростями 36 км/ч и 72 км/ч соответственно. На каком расстоянии окажутся друг от друга машины через 10 мин после встречи у перекрестка?
9. В безветренную погоду вертолет двигался со скоростью 90 км/ч точно на север. Найдите скорость вертолета, если подул северо-западный ветер под углом 45° к направлению движения. Скорость ветра 10 м/с.
10. Наблюдатель на берегу определил значение скорости пловца, переплывающего реку, 2,0 м/с. Скорость была направлена под углом 60° к линии берега. Какова скорость пловца относительно воды, если скорость течения реки 1,0 м/с?
11. По двум пересекающимся под углом 60° дорогам движутся два автомобиля с одинаковыми скоростями, равными 72 км/ч. Через какое время после встречи у перекрестка расстояние между ними станет равным 3 км?
Источник статьи: http://www.physbook.ru/index.php/%D0%97%D0%B0%D0%B4%D0%B0%D1%87%D0%B8._%D0%9E%D1%82%D0%BD%D0%BE%D1%81%D0%B8%D1%82%D0%B5%D0%BB%D1%8C%D0%BD%D0%BE%D1%81%D1%82%D1%8C_%D0%B4%D0%B2%D0%B8%D0%B6%D0%B5%D0%BD%D0%B8%D1%8F