Кинематика автомобиля
Кинематика касается вопросов движения тел в пространстве, и для автомобилистов этот раздел механики имеет огромное значение. Не секрет, что при прохождении поворотов у водителей зачастую возникают проблемы с выбором траектории движения транспортного средства, которые могут повлечь за собой самые негативные последствия. Именно поэтому следует уделить кинематике поворотов самое пристальное внимание
Аспекты, требующие особой внимательности
Понимание принципов движения колес автомобиля в повороте позволяет грамотно выполнять водителю все необходимые маневры даже в проблемных местах. Для наглядности можно выехать на участок дороги, на котором следы от колес будут хорошо заметны.
Сначала следует двигаться по прямой, а потом, вывернув колеса до упора, описать дугу. На прямом участке будут хорошо видны две полосы, а после начала поворота их окажется уже четыре. При этом задние колеса оставят следы ближе к центру поворота, а передние — ближе к его наружной части.
Чтобы понять суть такой картины, следует обратить внимание на такие аспекты:
- в начале движения передние колеса неизбежно уведут в сторону переднюю часть автомобиля;
- корпус машины начнет двигаться под углом относительно своего первоначального местоположения;
- в силу жесткого расположения относительно корпуса машины его задних колес, двигаться по аналогичной траектории начнут и они;
- задние колеса не будут идти по прямой вплоть до того места, где осуществят поворот передние;
- в повороте из-за этого движение автомобиля происходит полубоком, поэтому и появляются четыре следа от колес.
Такая особенность движения машины может стать причиной наезда на препятствия задними колесами или столкновения с различными объектами.
Максимальное срезание траектории и ее особенности
В процессе такого маневрирования водителю нельзя акцентировать внимание только на передней части автомобиля. У задних колес получается срезанная траектория, и разница между их следами и следами передних колес зависит от двух моментов:
- от угла поворота, совершаемого передними колесами;
- от расстояния между автомобильными осями (база).
При повороте колес до упора получается максимальное срезание траектории. Оно выражается в расстоянии между следами при выкручивании колес до упора. Зная это расстояние, водитель может рассчитать эту траекторию и, основываясь на имеющейся информации, выполнить необходимый ему маневр при подъезде к препятствию:
- если расстояние до объекта больше максимального срезания траектории – поворачивать колеса следует после его достижения передними колесами;
- если расстояние до объекта меньше максимального срезания траектории, – либо идти по прямой, либо не выворачивать колеса до упора;
- если до объекта практически не осталось места для маневра, поворот следует делать только по достижении препятствия осью задних колес.
Чем больше база, тем больше траектория срезания, поэтому у длинных и габаритных машин при прохождении поворота передние колеса зачастую выходят на встречную полосу, а задние соприкасаются с обочиной.
У автомобилей с большим задним свесом, когда имеется большое расстояние от задней оси до заднего габарита, встречается и другая проблема – при выполнении поворота идет выворачивание корпуса машины под определенным углом. При таком маневре корпуса вся передняя часть автомобиля уходит в сторону поворота, а задняя – в противоположную.
Если, к примеру, большой автобус совершает такой поворот, а рядом с ним находится легковой автомобиль, то задняя часть автобуса в ходе поворота неизбежно заденет его. Отсюда и четкое правило – никогда не следует вплотную прижиматься к габаритным транспортным средствам.
О практике грамотного прохождения поворотов
Попрактиковаться с прохождением поворотов можно, объезжая какой-нибудь статичный объект, например, столб или дерево. Схема поворота в этом случае следующая:
- сначала можно вплотную прижаться к объекту левым боком и совершить левый же поворот в тот момент, когда его оси достигли задние колеса;
- потом следует заранее просчитать боковое расстояние до объекта, которое больше максимальной траектории, после чего при достижении нужного места передними колесами можно совершать поворот.
Заранее выполнить расчет бокового расстояния до объекта сложно, и не всегда это получается сделать. Поэтому менее опытным водителям можно дать такой совет – совершая поворот, не нужно прижиматься вплотную к объекту, если же это произошло, – лучше отказаться от выполнения маневра.
Источник статьи: http://pvm-school.ru/articles/kinematika-avtomobilya/
Парадокс колеса
На приведённом рисунке хорошо видно, что все точки расположенные на радиусе колеса при совершении им одного оборота занимают те же самые места, на которых они были до начала вращения. Иными словами все точки радиуса колеса за один оборот перемещаются на одно и то же расстояние.
В то же время из школьного курса математики известно, что длина окружности равна:
Если прокатить колесо по поверхности и затем замерить пройденный им путь, то он будет точно соответствовать длине его окружности. Таким образом, две точки колеса: центр вращения и точка на внешней окружности проходят путь точно соответствующий приведённому расчёту. Но вот в отношении меньших радиусов мы приходим к выводу, что траектория их движения противоречит каноническому утверждению.
Так путь пройденный точкой, расположенной на половине радиуса колеса (r = R/2) должен быть равен:
C(r) = пиR, т.е. в половину меньше траектории точки расположенной на внешней окружности.
Но на самом деле она проходит фактически путь вдвое больший.
Соотношение фактически пройденной траектории и фактической дины окружности описываемый соответствующим радиусом растёт с уменьшением радиуса, фактически до бесконечности. Но в точке вращения он вновь возвращается к единице.
Самое удивительное в том, что если вырезать любую внутреннюю часть колеса и измерить его окружность, то она точно будет соответствовать вычисленной по канонической формуле.
Рассмотренный парадокс усиливается в случае, если колесо прокатывается с внешней стороны другой окружности. В этом случае траектория внутренних радиусов становится больше траектории точки на внешнем радиусе. И, наоборот, при прокатывании с внутренней стороны их траектория становится меньше.
Таким образом, можно сделать вывод о том, что траектория точек расположенных на внутренних радиусах колеса зависти не от величины собственного радиуса, а от радиуса внешней окружности. Что при этом происходит с материальными точками колеса расположенных на этих радиусах в пространстве остаётся загадкой.
Единственно разумное объяснение этого феномена предложил Галилей. Он считал, что поскольку фактическая траектория движения внутренних точек значительно больше фактической длины окружности, то точки внутренних радиусов проходят наблюдаемую траекторию с большей скоростью, чем это предписано им физикой [1]:
V = w*R, где w — угловая скорость вращения колеса.
Фактически линейная скорость внутренних точек колеса должна описываться уравнением:
V = n*w*r, где n = R/r
R – внешний радиус колеса;
r – внутренний радиус.
Иными словами линейная скорость точек внутренних радиусов является величиной постоянной и зависит только от внешнего радиуса колеса.
Вывод прямо скажем обескураживающий, но иного разумного объяснения пока ни кто не предложил.
Математически парадокс колеса в интерпретации Галилея описывается следующим уравнением:
dV = w*(R-r), где
dV – изменение скорости движения внутренних точек колеса;
R – внешний радиус колеса;
r – внутренний радиус колеса.
При r = R dV = 0
При r = 0 dV = w*R
Иными словами, изменение скорости точек расположенных на внутренних радиусах колеса меняется пропорционально от 0 на внешнем радиусе до V=w*R в центре вращения колеса. Поэтому ось колеса перемещается в пространстве с той же скоростью, которая соответствует линейной скорости вращающегося движения внешней окружности колеса при его прямолинейном движении. Соответственно такую же скорость имеют и все внутренние точки колеса.
С физической точки зрения полученный результат интерпретируется как движение жёсткого стержня, расположенного перпендикулярно направлению линейного движения оси вращения. Если рассмотреть движение такого стержня без привязки его к вращательному движению, то не трудно заметить, что все материальные точки стержня имеют одну и ту же скорость.
Преобразование вращательного движения в линейно-поступательное в данном случае решается методом рычага в рамках курса теоретической механики, которой к сожалению во времена Галилея ещё не существовало.
[1] Очевидно, именно по этому, этот парадокс практически не обсуждается в научной литературе.
Поскольку один из комментаторов так возбудился после прочтения этой статьи, что внёс меня в свои чёрные списки, и у меня нет возможности ему ответить иным путём, поэтому использую материал статьи не по назначению.
Сазонов Сергей 3 сентября 2019 года в 12:54
Писать рецензию на Вашу бредятину «Парадокс колеса» считаю излишним (много чести) — найдите в детском журнале «Квант» за 1975 год статью «ЦИКЛОИДА» . Там — примерно этот круг вопросов. Парадокса нет.
(конец цитаты)
К сожалению, найти указанный журнал в Интернете не смог, поэтому не смог лично ознакомиться со статьёй. Но уже само её название «ЦИКЛОИДА» говорит о том, Сергей Сазонов не видит разницы между прямой и циклоидой. В парадоксе колеса траектория меньшего радиуса разворачивается не в виде циклоиды, а в виде прямой линии. В этом то, как раз, и заключается парадокс. С другой стороны, то, что этим парадоксом интересовались Аристотель, Галилей, и возможно другие, не менее, замечательные умы человечества, говорит о том, что парадокс действительно существовал.
Уничижительное отношение к оппонентам явный признак ограниченной умственной деятельности. Конечно, можно было и не обращать внимание на подобные выпады, но, к сожалению, подобный уровень комментаторов встречается не так уж редко, поэтому считаю необходимым противостоять банальному хамству.
Источник статьи: http://proza.ru/2019/09/02/1746
Механическое движение. Траектория. Путь. Перемещение
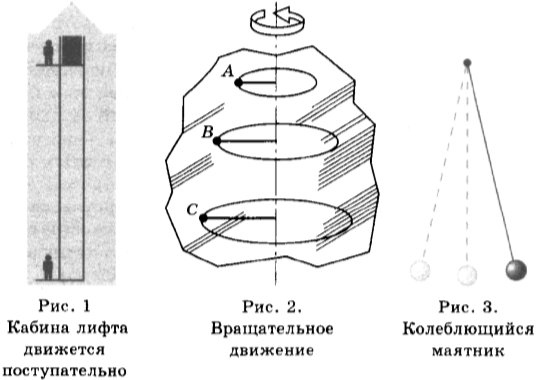
1. Механическим движением называют изменение положения тела в пространстве относительно других тел с течением времени. Существуют различные виды механического движения. Если все точки тела движутся одинаково и любая прямая, проведённая в теле, при его движении остаётся параллельной самой себе, то такое движение называется поступательным (рис. 1).
Точки вращающегося колеса описывают окружности относительно оси этого колеса. Колесо как целое и все его точки совершают вращательное движение (рис. 2).
Если тело, например шарик, подвешенный на нити, отклоняется от вертикального положения то в одну, то в другую сторону, то его движение является колебательным (рис. 3).
2. В определение понятия механического движения входят слова «относительно других тел». Они означают, что данное тело может покоиться относительно одних тел и двигаться относительно других тел. Так, пассажир, сидящий в автобусе, движущемся относительно зданий, тоже движется относительно них, но покоится относительно автобуса. Плот, плывущий по течению реки, неподвижен относительно воды, но движется относительно берега (рис. 4). Таким образом, говоря о механическом движении тела, необходимо указывать тело, относительно которого данное тело движется или покоится. Такое тело называют телом отсчёта. В приведённом примере с движущимся автобусом в качестве тела отсчёта может быть выбран какой-либо дом, или дерево, или столб около автобусной остановки.
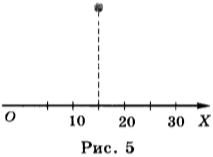
Для определения положения тела в пространстве вводят систему координат, которую связывают с телом отсчёта. При рассмотрении движения тела вдоль прямой линии используют одномерную систему координат, т.е. с телом отсчёта связывают одну координатную ось, например ось ОХ (рис. 5).
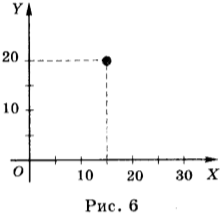
Если тело движется по криволинейной траектории, то система координат будет уже двухмерной, поскольку положение тела характеризуют две координаты X и Y (рис. 6). Таким движением является, например, движение мяча от удара футболиста или стрелы, выпущенной из лука.
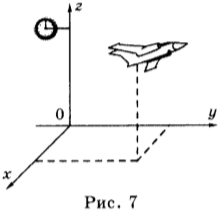
Если рассматривается движение тела в пространстве, например движение летящего самолёта, то система координат, связанная с телом отсчёта, будет состоять из трёх взаимно перпендикулярных координатных осей (OX, OY и OZ) (рис. 7).
Поскольку при движении тела его положение в пространстве, т.е. его координаты, изменяются с течением времени, то необходим прибор (часы), который позволяет измерять время и определить, какому моменту времени соответствует та или иная координата.
Таким образом, для определения положения тела в пространстве и изменения этого положения с течением времени необходимы тело отсчёта, связанная с ним система координат и способ измерения времени, т.е. часы, которые все вместе представляют собой систему отсчёта (рис. 7).
3. Изучить движение тела — это значит определить, как изменяется его положение, т.е. координата, с течением времени.
Если известно, как изменяется координата со временем, можно определить положение (координату) тела в любой момент времени.
Основная задача механики состоит в определении положения (координаты) тела в любой момент времени.
Чтобы указать, как изменяется положение тела с течением времени, нужно установить связь между величинами, характеризующими это движение, т.е. найти математическое описание движения или, иными словами, записать уравнение движения тела.
Раздел механики, изучающий способы описания движения тел, называют кинематикой.
4. Любое движущееся тело имеет определённые размеры, и его различные части занимают разные положения в пространстве. Возникает вопрос, как в таком случае определить положение тела в пространстве. В делом ряде случаев нет необходимости указывать положение каждой точки тела и для каждой точки записывать уравнение движения.
Так, поскольку при поступательном движении все точки тела движутся одинаково, то нет необходимости описывать движение каждой точки тела.
Движение каждой точки тела не нужно описывать и при решении таких задач, когда размерами тела можно пренебречь. Например, если нас интересует, с какой скоростью пловец проплывает свою дистанцию, то рассматривать движение каждой точки пловца нет необходимости. Если же необходимо определить действующую на мяч выталкивающую силу, то пренебречь размерами пловца уже нельзя. Если мы хотим вычислить время движения космического корабля от Земли до космической станции, то корабль можно считать единым целым и представить в виде некоторой точки. Если же рассчитывается режим стыковки корабля со станцией, то, представив корабль в виде точки, решить эту задачу невозможно.
Таким образом, для решения ряда задач, связанных с движением тел, вводят понятие материальной точки.
Материальной точкой называют тело, размерами которого можно пренебречь в условиях данной задачи.
В приведённых выше примерах материальной точкой можно считать пловца при расчёте скорости его движения, космический корабль при определении времени его движения.
Материальная точка — это модель реальных объектов, реальных тел. Считая тело материальной точкой, мы отвлекаемся от несущественных для решения конкретной задачи признаков, в частности, от размеров тела.
5. При перемещении тело последовательно проходит точки пространства, соединив которые, можно получить линию. Эта линия, вдоль которой движется тело, называется траекторией. Траектория может быть видимой или невидимой. Видимую траекторию описывают трамвай при движении по рельсам, лыжник, скользя по лыжне, мел, которым пишут на доске. Траектория летящего самолёта в большинстве случаев невидима, невидимой является траектория ползущего насекомого.
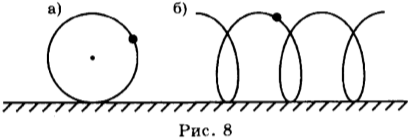
Траектория движения тела относительна: её форма зависит от выбора системы отсчёта. Так, траекторией точек обода колеса велосипеда, движущегося по прямой дороге, относительно оси колеса является окружность, а относительно Земли — винтовая линия (рис. 8 а, б).
6. Одной из характеристик механического движения является путь, пройденный телом. Путём называют физическую величину, равную расстоянию, пройденному телом вдоль траектории.
Если известны траектория тела, его начальное положение и пройденный им путь за время \( t \) , то можно найти положение тела в момент времени \( t \) . (рис. 9)
Путь обозначают буквой \( l \) (иногда \( s \) ), основная единица пути 1 м: \( [\,\mathrm
Путь — величина относительная, значение пути зависит от выбора системы отсчёта. Так, путь пассажира, переходящего из конца движущегося автобуса к его передней двери, равен длине автобуса в системе отсчёта, связанной с автобусом. В системе отсчёта, связанной с Землёй, он равен сумме длины автобуса и пути, который проехал автобус относительно Земли.
7. Если траектория движения тела неизвестна, то значение пути не позволит установить его положение в любой момент времени, поскольку направление движения тела не определено. В этом случае используют другую характеристику механического движения — перемещение.
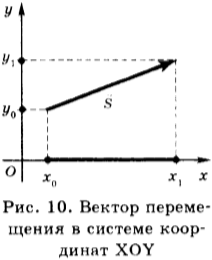
Перемещение — вектор, соединяющий начальное положение тела с его конечным положением (рис. 10)
Перемещение — векторная физическая величина, имеет направление и числовое значение, обозначается \( \overrightarrow \) . Единица перемещения \( [\,\mathrm\,] \) = 1 м.
Зная начальное положение тела, его перемещение (направление и модуль) за некоторый промежуток времени, можно определить положение тела в конце этого промежутка времени.
Следует иметь в виду, что перемещение в общем случае не совпадает с траекторией, а модуль перемещения — с пройденным путём. Это совпадение имеет место лишь при движении тела по прямолинейной траектории в одну сторону. Например, если пловец проплыл 100-метровую дистанцию в бассейне, длина дорожки которого 50 м, то его путь равен 100 м, а модуль перемещения равен нулю.
Перемещение, так же как и путь, величина относительная, зависит от выбора системы отсчёта.
При решении задач пользуются проекциями вектора перемещения. На рисунке 10 изображены система координат и вектор перемещения в этой системе координат.
Координаты начала перемещения — \( x_0, y_0 \) ; координаты конца перемещения — \( x_1, y_1 \) . Проекция вектора перемещения на ось ОХ равна: \( s_x=x_1-x_0 \) . Проекция вектора перемещения на ось OY равна: \( s_y=y_1-y_0 \) .
Модуль вектора перемещения равен: \( s=\sqrt
ПРИМЕРЫ ЗАДАНИЙ
Часть 1
1. В состав системы отсчёта входят
1) только тело отсчёта
2) только тело отсчёта и система координат
3) только тело отсчёта и часы
4) тело отсчёта, система координат, часы
2. Относительной величиной является: А. Путь; Б. Перемещение. Правильный ответ
1) только А
2) только Б
3) и А, и Б
4) ни А, ни Б
3. Пассажир метро стоит на движущемся вверх эскалаторе. Он неподвижен относительно
1) пассажиров, стоящих на другом эскалаторе, движущемся вниз
2) других пассажиров, стоящих на этом же эскалаторе
3) пассажиров, шагающих вверх по этому же эскалатору
4) светильников на баллюстраде эскалатора
4. Относительно какого тела покоится автомобиль, движущийся по автостраде?
1) относительно другого автомобиля, движущегося с такой же скоростью в противоположную сторону
2) относительно другого автомобиля, движущегося с такой же скоростью в ту же сторону
3) относительно светофора
4) относительно идущего вдоль дороги пешехода
5. Два автомобиля движутся с одинаковой скоростью 20 м/с относительно Земли в одном направлении. Чему равна скорость одного автомобиля в системе отсчёта, связанной с другим автомобилем?
1) 0
2) 20 м/с
3) 40 м/с
4) -20 м/с
6. Два автомобиля движутся с одинаковой скоростью 15 м/с относительно Земли навстречу друг другу. Чему равна скорость одного автомобиля в системе отсчёта, связанной с другим автомобилем?
1) 0
2) 15 м/с
3) 30 м/с
4) -15 м/с
7. Какова относительно Земли траектория точки лопасти винта летящего вертолёта?
1) прямая
2) окружность
3) дуга
4) винтовая линия
8. Мяч падает с высоты 2 м и после удара о пол поднимается на высоту 1,3 м. Чему равны путь \( l \) и модуль перемещения \( s \) мяча за всё время движения?
1) \( l \) = 3,3 м, \( s \) = 3,3 м
2) \( l \) = 3,3 м, \( s \) = 0,7 м
3) \( l \) = 0,7 м, \( s \) = 0,7 м
4) \( l \) = 0,7 м, \( s \) = 3,3 м
9. Решают две задачи. 1. Рассчитывают скорость движения поезда между двумя станциями. 2. Определяют силу трения, действующую на поезд. При решении какой задачи поезд можно считать материальной точкой?
1) только первой
2) только второй
3) и первой, и второй
4) ни первой, ни второй
10. Точка обода колеса при движении велосипеда описывает половину окружности радиуса \( R \) . Чему равны при этом путь \( l \) и модуль перемещения \( s \) точки обода?
1) \( l=2R \) , \( s=2R \)
2) \( l=\pi R \) , \( s=2R \)
3) \( l=2R \) , \( s=\pi R \)
4) \( l=\pi R \) , \( s=\pi R \) .
11. Установите соответствие между элементами знаний в левом столбце и понятиями в правом столбце. В таблице под номером элемента знаний левого столбца запишите соответствующий номер выбранного вами понятия правого столбца.
ЭЛЕМЕНТ ЗНАНИЙ
A) физическая величина
Б) единица величины
B) измерительный прибор
ПОНЯТИЕ
1) траектория
2) путь
3) секундомер
4) километр
5) система отсчёта
12. Установите соответствие между величинами в левом столбце и характером величины в правом столбце. В таблице под номером элемента знаний левого столбца запишите соответствующий номер выбранного вами понятия правого столбца.
ВЕЛИЧИНА
A) путь
Б) перемещение
B) проекция перемещения
ХАРАКТЕР ВЕЛИЧИНЫ
1) скалярная
2) векторная
Часть 2
13. Автомобиль свернул на дорогу, составляющую угол 30° с главной дорогой, и совершил по ней перемещение, модуль которого равен 20 м. Определите проекцию перемещения автомобиля на главную дорогу и на дорогу, перпендикулярную главной дороге.
Источник статьи: http://fizi4ka.ru/ogje-2018-po-fizike/mehanicheskoe-dvizhenie-traektorija-put-peremeshhenie.html