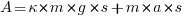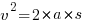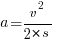- Определение работы двигателя автомобиля
- Работа, мощность, КПД
- Работы силы, формула
- Работа — разность кинетической энергии
- Работа силы тяжести — разность потенциальной энергии
- Мощность
- Еще одна формула для расчета мощности
- Моточасы двигателя машины — что это и зачем нужно?
- Почему важно знать количество моточасов?
- Как рассчитать количество моточасов?
Определение работы двигателя автомобиля



Необходимо: определить работу двигателя, равноускорено движущегося автомобиля. Известно, что на участке пути равном ста метрам, автомобиль развил скорость сто восемь километров в час (тридцать метров в секунду), масса автомобиля две тысячи килограмм, коэффициент трения равен ноль целых пять сотых.
Дано: s=100 м; v=20 м/сек; m=2000 кг; κ=0,05
Найти: A-?
Запишем формулу для определения работы
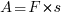
где F – сила тяги, а s – путь.
Сила тяги состоит из силы 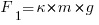
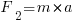
Формула для определения работы двигателя автомобиля принимает вид
Ускорение a найдем из формулы
Получаем итоговую формулу работы и производим расчет
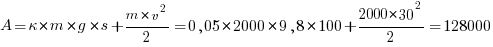
Ответ: работа двигателя равноускорено движущегося автомобиля равна 128000 джоуль.
Источник статьи: http://studopedia.ru/11_72720_opredelenie-raboti-dvigatelya-avtomobilya.html
Работа, мощность, КПД
Сила, перемещающая тело, совершает работу. Работа – это разность энергии тела в начале процесса и в его конце. А мощность – это работа за одну секунду. Коэффициент полезного действия (КПД) – это дробное число. Максимальный КПД равен единице, однако, часто, КПД меньше единицы.
Работы силы, формула
Сила, приложенная к телу и перемещающая его, совершает работу (рис. 1).
Работа силы — это скалярное произведение вектора силы на вектор перемещения.
Работу, совершаемую силой, можно посчитать, используя векторный или скалярный вид записи такой формулы:
Векторный вид записи
Для решения задач правую часть этой формулы удобно записывать в скалярном виде:
\[ \large \boxed < A = \left| \vec\right| \cdot cos(\alpha) >\]
\( F \left( H \right) \) – сила, перемещающая тело;
\( S \left( \text <м>\right) \) – перемещение тела под действием силы;
\( \alpha \) – угол между вектором силы и вектором перемещения тела;
Работу обозначают символом \(A\) и измеряют в Джоулях. Работа – это скалярная величина.
В случае, когда сила постоянная, формула позволяет рассчитать работу, совершенную силой за полное время ее действия.
Если сила изменяется со временем, то в каждый конкретный момент времени будем получать мгновенную работу. Эти, мгновенные значения для разных моментов времени будут различаться.
Рассмотрим несколько случаев, следующих из формулы:
- Когда угол между силой и перемещением острый, работа силы положительная;
- А если угол тупой — работа отрицательная, так как косинус тупого угла отрицательный;
- Если же угол прямой – работа равна нулю. Сила, перпендикулярная перемещению, работу не совершает!
Работа — разность кинетической энергии
Работу можно рассчитать еще одним способом — измеряя кинетическую энергию тела в начале и в конце процесса движения. Рассмотрим такой пример. Пусть автомобиль, движется по горизонтальной прямой и, при этом увеличивает свою скорость (рис. 2). Масса автомобиля 1000 кг. В начале его скорость равнялась 1 м/с. После разгона скорость автомобиля равна 10 метрам в секунду. Найдем работу, которую пришлось проделать, чтобы ускорить этот автомобиль.
Для этого посчитаем энергию движения автомобиля в начале и в конце разгона.
\( E_
\( E_
\( m \left( \text<кг>\right) \) – масса автомобиля;
\( \displaystyle v \left( \frac<\text<м>>
Кинетическую энергию будем вычислять, используя формулу:
\[ \large E_
\[ \large E_
Теперь найдем разницу кинетической энергии в конце и вначале разгона.
\[ \large \Delta E_
\[ \large \Delta E_
Значит, работа, которую потребовалось совершить, чтобы разогнать машину массой 1000 кг от скорости 1 м/с до скорости 10 м/с, равняется 49500 Джоулям.
Примечание: Работа – это разность энергии в конце процесса и в его начале. Можно находить разность кинетической энергии, а можно — разность энергии потенциальной.
Работа силы тяжести — разность потенциальной энергии
Рассмотрим теперь следующий пример. Яблоко массой 0,2 кг упало на садовый стол с ветки, находящейся на высоте 3 метра от поверхности земли. Столешница располагается на высоте 1 метр от поверхности (рис. 3). Найдем работу силы тяжести в этом процессе.
Посчитаем потенциальную энергию яблока до его падения и энергию яблока на столешнице.
\( E_
\( E_
Примечание: Работу можно рассчитать через разность потенциальной энергии тела.
Потенциальную энергию будем вычислять, используя формулу:
\[ \large E_
= m \cdot g \cdot h\]
\( m \left( \text<кг>\right) \) – масса яблока;
\( h \left( \text<м>\right) \) – высота, на которой находится яблоко относительно поверхности земли.
Начальная высота яблока над поверхностью земли равна 3 метрам
\[ \large E_
Потенциальная энергия яблока на столе
\[ \large E_
Теперь найдем разницу потенциальной энергии яблока в конце падения и перед его началом.
\[ \large \Delta E_
= E_
\[ \large \Delta E_
= 2 – 6 = — 4 \left(\text <Дж>\right) \]
Важно помнить: Когда тело падает на землю, его потенциальная энергия уменьшается. Сила тяжести при этом совершает положительную работу!
Чтобы работа получилась положительной, в правой части формулы перед \( \Delta E_
\) дополнительно допишем знак «минус».
Значит, работа, которую потребовалось совершить силе тяжести, чтобы яблоко массой 0,2 кг упало с высоты 3 м на высоту 1 метр, равняется 4 Джоулям.
Примечания:
- Если тело падает на землю, работа силы тяжести положительна;
- Когда мы поднимаем тело над землей, мы совершаем работу против силы тяжести. Наша работа при этом положительна, а работа силы тяжести будет отрицательной;
- Сила тяжести относится к консервативным силам. Для консервативных сил перед разностью потенциальной энергии мы дописываем знак «минус»;
- Работа силы тяжести не зависит от траектории, по которой двигалось тело;
- Работа для силы \(\displaystyle F_<\text<тяж>>\) зависит только от разности высот, в которых тело находилось в конечный и начальный моменты времени.
Рисунок 4 иллюстрирует факт, что для силы \(\displaystyle F_<\text<тяж>>\) работа зависит только от разности высот и не зависит от траектории, по которой тело двигалось.
Мощность
В механике мощность часто обозначают символами N или P и измеряют в Ваттах в честь шотландского изобретателя Джеймса Уатта.
Примечание: Символ \(\vec
Мощность – это работа, совершенная за одну секунду (энергия, затраченная за 1 сек).
Расчет работы осуществляем, используя любую из формул:
\[ \large A = \Delta E_
\[ \large A = \Delta E_
\]
\[ \large A = F \cdot S \cdot cos(\alpha) \]
Разделив эту работу на время, в течение которого она совершалась, получим мощность.
Если работа совершалась равными частями за одинаковые интервалы времени – мощность будет постоянной величиной.
Мощность переменная, когда в некоторые интервалы времени совершалось больше работы.
Еще одна формула для расчета мощности
Есть еще один способ расчета мощности, когда сила перемещает тело и при этом скорость тела не меняется:
\[ \large P = \left( \vec
Формулу можно записать в скалярном виде:
\[ \large P = \left| \vec
\( F \left( H \right) \) – сила, перемещающая тело;
\( \displaystyle v \left( \frac<\text<м>>
\( \alpha \) – угол между вектором силы и вектором скорости тела;
Когда векторы \(\vec
Примечание: Такую формулу для расчета мощности можно получить из выражения для работы силы, разделив обе части этого выражения на время, в течение которого работа совершалась (а если точнее, найдя производную обеих частей уравнения).
КПД – коэффициент полезного действия. Обычно обозначают греческим символом \(\eta\) «эта». Единиц измерения не имеет, выражается либо десятичной дробью, либо в процентах.
Примечания:
- Процент – это дробь, у которой в знаменателе число 100.
- КПД — это либо правильная дробь, или дробь, равная единице.
Вычисляют коэффициент \(\eta\) для какого-либо устройства, механизма или процесса.
\( \large A_<\text<полезная>> \left(\text <Дж>\right)\) – полезная работа;
\(\large A_<\text<вся>> \left(\text <Дж>\right)\) – вся затраченная для выполнения работы энергия;
Примечание: КПД часто меньше единицы, так как всегда есть потери энергии. Коэффициент полезного действия не может быть больше единицы, так как это противоречит закону сохранения энергии.
Величина \(\eta\) является дробной величиной. Если числитель и знаменатель дроби разделить на одно и то же число, полученная дробь будет равна исходной. Используя этот факт, можно вычислять КПД, используя мощности:
Источник статьи: http://formulki.ru/mehanika/rabota-moshhnost-kpd
Моточасы двигателя машины — что это и зачем нужно?
Моточасы – единица измерения фактически отработанного времени двигателя с учетом среднего количества оборотов коленвала. Данный параметр может быть рассчитан для любого типа ДВС (двигателей внутреннего сгорания): бензиновые, дизельные, двухтактные и т.д. В отношении легкового автомобиля моточас позволяет понять реальный износ мотора – это более объективный показатель, чем километраж. Например, жители мегаполисов много времени проводят в пробках, километраж не растет, а износ двигателя увеличивается.
Почему важно знать количество моточасов?
На автосервисах и центрах замены масла всегда указывается километраж, наездив который водителю нужно менять моторное масло. Обычно – это 10 000 – 15 000 км, хотя фактически периодичность замены зависит от моточасов. Например, в лодочных моторах масло меняют только по данному параметру, без учета километража. Тем более стоит учесть, что у каждого авто свои особенности эксплуатации и если машина часто стоит в пробках, масло раньше выработает свой ресурс, что на долгой дистанции приведет к появлению проблем с мотором.Указание километража имеет смысл, если он будет наезжен в идеальном смешанном цикле, без длительных простоев авто в пробках и прогревов в зимнее время.
На основании независимого исследования были опубликованы данные по выработке ресурса масла в моточасах, в зависимости от его типа:
- Минеральное масло – 150 часов;
- Полусинтетическое масло – 250 часов;
- Синтетическое масло – от 250 до 450 часов в зависимости от класса.
В случае превышения указанного ресурса все полезные свойства масла заканчиваются, что сильно увеличит износ двигателя автомобиля.
Как рассчитать количество моточасов?
Продолжительность идеального моточаса приравнена к астрономическому часу (60 минутам), но она зависит от количества оборотов коленвала. В качестве идеального значения, берут средние обороты, с учетом холостого хода авто при прогреве мотора, езды по городу, трассе и т.д. Соответственно, если автомобиль стоит в пробке и работает на холостых оборотах, продолжительность моточаса будет более 60 минут. Если авто едет по трассе а обороты в районе 2 000 – 3 000, продолжительность моточаса менее 60 минут.
Есть 4 способа рассчитать выработанные моточасы для авто:
- На некоторых современных немецких автомобилях бортовой компьютер самостоятельно считает параметр и выводит информацию на экран, но практика автоматического подсчета моточасов еще не до конца закрепилась у производителей.
- Подсчет на основе средней скорости. Также подходит не для всех авто. Актуально, если бортовой компьютер показывает среднюю скорость за определенный отрезок времени (километраж). Чтобы получить объективные данные, рекомендуется наездить не менее 1 500 – 2 000 км. Тогда расчет проводится по формуле: Р=S*М, где Р – периодичность замены масла в километраже, S – средняя скорость авто, М – количество моточасов до выработки рабочего ресурса масла. Например, средняя скорость машины – 35 км/ч, а в двигатель заливается полусинтетическое масло с ресурсом в 250 моточасов. В таком случае 35*250=8 750 км. Наездив данный километраж, водителю рекомендовано заменить масло.
- Подсчет на основе расхода топлива. Здесь нужно знать норматив расхода топлива для авто в смешанном цикле и рекомендуемая производителем периодичность замены масла в километраже. Например, OpelOmegaB с дизельным двигателем 2.2 в смешанном цикле расходует 6.9 литра топлива на 100 км. В мотор залито масло с рекомендованным километражом в 15 000. Тогда 15 000 делим на 6.9 и получаем 2 174 литра топлива. Как только указанное количество солярки будет израсходовано – масло нужно менять.
- Использование специальных датчиков.
Есть несколько видов таких датчиков:
- Электромеханические и электронные (работают по принципу обычных часов, считают только время работы двигателя, без учета оборотов коленвала). Подключаются к стационарной автомобильной розетке, срабатывают при включении зажигания.
- Вибрационный. С помощью двухстороннего скотча счетчик крепится на двигатель. При заводке автомобиля, сенсор воспринимает вибрации от мотора и срабатывает. Также считает только время работы двигателя, без учета оборотов коленвала.
- Счетчик, активируемый импульсами. Обладает встроенным тахометром. Срабатывает при подаче импульсов от системы зажигания. Самый распространенный вариант подключения – наматывание нескольких витков сигнального кабеля на высоковольтные провода. Отличается наибольшей точностью подсчета.
Источник статьи: http://zen.yandex.ru/media/rudorogi/motochasy-dvigatelia-mashiny—chto-eto-i-zachem-nujno-5d7b4096aad4363eae52c635