Какая сила трения действует между ведущим колесом автомобиля
2017-12-15 
Как направлена сила трения, действующая на ведущие колеса автомобиля, при разгоне (а), торможении (б), повороте (в)? Равна ли эта сила своему максимальному значению $\mu N$ ($\mu$ — коэффициент трения, $N$ — сила реакции полотна дороги), и если да, то в каких ситуациях? А в каких ситуациях нет? Хорошо это, или плохо, если сила трения достигает своего максимального значения? Почему? Какой автомобиль может развивать на дороге большую мощность — передне- или заднеприводный — при одинаковой мощности мотора и почему? Считать, что масса автомобиля распределена равномерно, и его центр тяжести находится посередине.
Обсудим сначала вопрос о роли силы трения в движении машины. Представим себе, что водитель машины, стоящей на гладком-гладком льду (сила трения между колесами и льдом отсутствует), нажимает на педаль газа. Что будет происходить? Ясно, что машина ехать не будет: колеса будут вращаться, но будут пробуксовывать относительно льда — ведь трения-то нет. Причем это будет происходить независимо от мощности двигателя. А это значит, что для того, чтобы мощность двигателя использовать, нужно трение — без него машина не поедет.
Что же происходит, когда сила трения есть. Пусть сначала она очень маленькая, а водитель стоящей машины снова нажимает на педаль газа? Колеса (речь сейчас идет о ведущих колесах автомобиля, допустим это передние колеса) проскальзывают относительно поверхности (трение — маленькое), вращаясь так, как показано на рисунке, но при этом возникает сила трения, действующая со стороны дороги на колеса, направленная вперед по ходу движения машины. Она и толкает машину вперед.
Если сила трения большая, то при плавном нажатии на педаль газа колеса начинают вращаться, и как бы отталкиваются от шероховатостей дороги, используя силу трения, которая направлена вперед. При этом колеса не проскальзывают, а катятся по дороге, так, что нижняя точка колеса не перемещается относительно полотна. Иногда и при большом трении колеса пробуксовывают. Наверняка, вы сталкивались с ситуацией, когда какой-нибудь «сумасшедший водитель» так трогается при включении зеленого сигнала светофора, что колеса «визжат», а на дороге остается черный след из-за скольжения резины по асфальту. Итак, в экстренной ситуации (при резком торможении или трогании с побуксовкой) колеса скользят относительно дороги, в обычных случаях (когда на дороге не остается черного следа от стирающихся покрышек) колесо не скользит, а только катится по дороге.
Итак, если машина едет равномерно, то колеса не скользят по дороге, а катятся по ней так, что нижняя точка колеса покоится (а не проскальзывает) относительно дороги. Как в этом случае направлена сила трения? Сказать, что противоположно скорости машины — неверно, ведь говоря так про силу трения, подразумевают случай скольжения тела относительно поверхности, а сейчас у нас скольжения колес относительно дороги нет. Сила трения в этом случае может быть направлена как угодно, и мы сами определяем ее направление. И вот как это происходит.
Представим себе, что нет никаких препятствующих движению машины факторов. Тогда машина движется по инерции, колеса вращаются по инерции, причем угловая скорость вращения колес связана со скоростью движения машины. Установим эту связь. Пусть колесо движется со скоростью $v$ и вращается так, что нижняя точка колеса не проскальзывает относительно дороги. Перейдем в систему отсчета, связанную с центром колеса. В ней колесо как целое не движется, а только вращается, а земля движется назад со скоростью $v$. Но поскольку колесо не проскальзывает относительно земли, то его нижняя точка имеет такую же скорость как земля. А значит, и все точки поверхности колеса вращаются относительно центра со скоростью $v$ и, следовательно, имеют угловую скорость $\omega = v / R$, где R — радиус колеса. Переходя теперь назад в систему отсчета, связанную с землей, заключаем, что при отсутствии проскальзывания между нижней точкой колеса и дорогой угловая скорость колеса $\omega = v / R$, а все точки поверхности имеют разные скорости относительно земли: например, нижняя точка — нулевую, верхняя $2v$ и т. д.
А пусть водитель при таком движении машины нажимает на педаль газа. Он заставляет колесо вращаться быстрее, чем нужно при данной скорости машины. Колесо стремится проскользнуть назад, возникает сила трения, направленная вперед, которая и разгоняет машину (машина как бы отталкивается от шероховатостей дороги, используя силу трения). Если водитель нажимает на педаль тормоза, колесо стремится вращаться медленнее, чем нужно при данной скорости машины. Возникает сила трения, направленная назад, которая тормозит машину. Если водитель поворачивает колеса машины, возникает сила трения, направленная в сторону поворота, которая машину поворачивает. Таким образом, управление машиной — разгоном, торможением, поворотом — основано на правильном использовании силы трения, причем, конечно, подавляющее большинство водителей об этом даже не догадываются.
Ответим теперь на вопрос: равна ли эта сила своему максимальному значению? Вообще говоря, нет, поскольку нет скольжения колеса относительно дороги, а сила трения равна максимальному значению при скольжении. В покое сила трения может принимать любые значения от нуля до максимального $\mu N$, где $\mu$ — коэффициент трения; $N$ — сила реакции опоры. Поэтому если мы разгоняемся (сила трения направлена вперед), но хотим увеличить темп разгона, мы сильнее нажимаем на педаль газа, и увеличиваем силу трения. Аналогично, если мы тормозим (сила трения направлена назад), но хотим увеличить степень торможения, мы сильнее нажимаем на тормоз и увеличиваем силу трения. Но ясно, что ее можно увеличить и в том и в другом случае, если она не была максимальной! Таким образом, для управления машиной сила трения не должна равняться максимальному значению, и эту разность мы используем для совершения тех или иных маневров. И любой водитель (даже если он ничего не знает про силу трения, а таких, конечно, подавляющее большинство) интуитивно чувствует, есть ли у него резерв силы трения, «далеко» ли машина от пробуксовки, и есть ли возможность ей управлять.
Тем не менее, есть одна ситуация, когда сила трения равна своему максимальному значению. Эта ситуация называется заносом. Пусть водитель резко затормозил на скользкой дороге. Машина начинает скользить по дороге, это состояние движения и называется заносом. В этом случае сила трения направлена противоположно скорости (назад) и равна своему максимальному значению. Это ситуация очень опасна, ведь машина АБСОЛЮТНО неуправляема. Мы не можем повернуть (хоть как-то, хоть чуть-чуть), ведь для поворота нам нужна сила трения, направленная в сторону поворота, а в нашем распоряжении ее нет — сила трения максимальна и направлена назад. Мы не можем увеличить скорость торможения (невозможно увеличить силу трения — она и так максимальна), не можем (даже если бы мы захотели этого в такой ситуации) ускориться. Мы не можем ничего! Ситуация осложняется еще и тем, что в состоянии заноса машину никто не «держит» на дороге. Почему машина в обычных условиях не съезжает в кювет, ведь полотно дороги всегда делается покатым к обочинам, чтобы стекала вода? Ее держит сила трения, а вот если машина скользит (занос) сила трения направлена противоположно скорости и никак иначе. Поэтому любое «боковое» возмущение — покатость дороги, небольшой камень под одним из колес — могут развернуть или сбросить машину на обочину. Никогда не допускайте заноса1.
Теперь сравним мощность, которую могут развивать на дороге передне- и заднеприводной автомобили с одинаковым мотором. Очевидно, что мощность, которую может развивать автомобиль на дороге, зависит не только от его двигателя, но и от того, как автомобиль «использует» силу трения. Действительно, в отсутствие силы трения автомобиль стоял бы на месте (с вращающимися колесами) независимо от мощности двигателя (вращающего эти колеса). Докажем, что заднеприводные автомобили мощнее переднеприводных при одинаковой мощности мотора и оценим отношение мощностей, которые может развивать двигатель, разгоняя машину на дороге (при условии, что мощность самого двигателя может быть очень большой).
Разгоняет автомобиль сила трения, действующая на ведущие колеса, а она не может превышать значения $\mu N$ ($N$ — сила реакции). Поэтому чем больше сила реакции, тем больших значений может достигнуть разгоняющая сила трения (а нажатие на педаль газа в ситуации, когда сила трения достигла максимума, приведет только к проскальзыванию и к заносу, но не к увеличению мощности, которую развивает двигатель). Найдем силы реакции для задних и передних колес машины. Силы, действующие на машину при разгоне, показаны на рисунках (на правом — для заднеприводной, на левом — для переднеприводной). На машину действуют: сила тяжести, силы реакции и сила трения. Поскольку машина движется поступательно, сумма моментов всех сил относительно ее центра тяжести равна нулю. Поэтому, если центр тяжести машины находится точно посередине машины, расстояние между задними и передними колесами $l$, а высота центра тяжести над дорогой $h$, условие равенства нулю суммы моментов относительно центра тяжести дает (при условии, что машина движется, развивая максимальную мощность на максимуме силы трения):
$N_ <1>\frac
$N_ <1>\frac
где $\mu$ — коэффициент трения. Учитывая, что и в том и в другом случае $N_ <1>+ N_ <2>= mg$, из (1) найдем силу реакции для передних колес в случае переднеприводного автомобиля
и из (2) силу реакции задних колес в случае заднего привода
(здесь (пп) и (зп) — передний и задний привод). Отсюда находим отношение сил трения, разгоняющих передне- и заднеприводную машину, и, следовательно, отношение мощностей, которые может развивать на дороге их двигатель
Для значений $l = 3 м, h = 0,5 м$ и $\mu = 0,5$ имеем из (5)
Источник статьи: http://earthz.ru/solves/Zadacha-po-fizike-5700
Колесо и дорога. Силы действующие на колесо
Как будто все просто: вращение вала автомобильного двигателя, переданное через механизмы силовой передачи, заставляет вращаться колеса, колеса катятся по дороге; оси вращения при перекатывании колес перемещаются вперед; оси так или иначе связаны с рамой и кузовом автомобиля; значит, вместе с осями перемещается и кузов, и автомобиль. Однако такого описания недостаточно. Необходимо знать, какие силы действуют на колесо. Вот они:
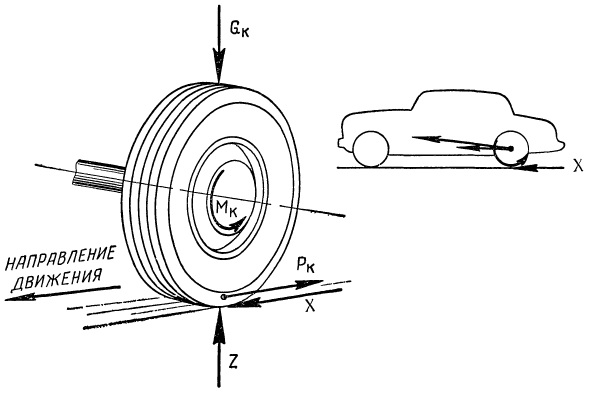
- вращающий момент Мк, заставляющий колесо вращаться и создающий тяговую силу Рк
- сила тяжести, соответствующая нагрузке на колесо Gk
- вертикальная реакция дороги Z и горизонтальная X, действующая в направлении движения (т.е. обратном действию силы Рк).
Тяговая сила Рк (в кг) равна подводимому к колесам вращающему моменту Мк (в кгм), деленному на радиус качения колеса (в м):
Момент Мк зависит от крутящего момента двигателя Ме, передаточных чисел в системе силовой передачи и коэффициента полезного действия n силовой передачи, который для обычных автомобилей равен 0,9. Чем больше передаточные числа в коробке передач и в заднем мосту, тем больше подводимый к колесам вращающий момент:
где iк — передаточное число в коробке передач;
i0 — передаточное число главной передачи.
Рис. Слева — силы, действующие на колесо. Справа — дорога толкает колесо, ось перемещается вперед и толкает рессоры, рессоры толкают кузов.
Таким образом, тяговая сила на ведущих колесах автомобиля:
Теперь можно высказать два на первый взгляд неожиданных положения:
- Движение колеса происходит под действием силы (реакции) X, т. е. дорога толкает автомобиль. Выше был приведен пример действия силы прыгуна на площадку и силы противодействия площадки. Точно так же и ведущее колесо автомобиля отталкивает от себя назад дорогу с силой Рк, а дорога противодействует этому силой (реакцией) X. Реакция X толкает вперед колесо, а оно через ось и подвеску толкает вперед весь автомобиль.
- В каждое отдельно взятое мгновение ближайшие к дороге точки колеса неподвижны, не перемещаются относительно поверхности дороги. Более того, если бы они перемещались, автомобиль не двигался бы, а колесо скользило бы по поверхности дороги. Происходило бы то, что называется на языке автомобилистов буксованием колеса.
Чтобы точки контакта колеса с дорогой были неподвижными, требуется хорошее сцепление шины с поверхностью дороги.
Сцепление шины с дорогой оценивают так называемым коэффициентом сцепления Ф («фи»).
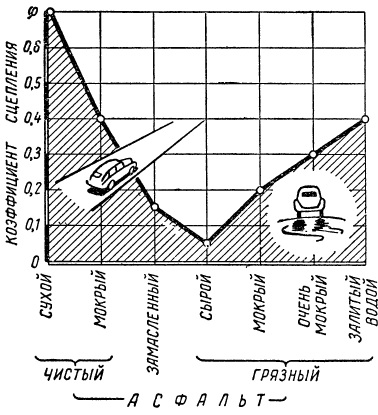
Рис. Величина коэффициента сцепления зависит от состояния поверхности дороги.
Коэффициент сцепления равен отношению наибольшей величины реакции X (при проскальзывании, буксовании колеса) к величине реакции Z:
Величина коэффициента сцепления Ф колеблется в пределах 0,5—0,8 для сухих твердых дорог и 0,15—0,4 для обледенелых или мокрых. Из приведенного графика видно, как влияет состояние поверхности асфальтовой дороги на коэффициент сцепления.
Коэффициент сцепления на сухой дороге лишь незначительно изменяется в зависимости от изменений нагрузки на колесо, давления в шине и скорости движения, но на мокрой или обледенелой дороге с увеличением скорости происходит резкое уменьшение коэффициента сцепления, так как шина не успевает выдавливать влагу, находящуюся в области контакта шины с дорогой, и остающаяся пленка влаги облегчает скольжение шины.
Необходимое для движения сцепление шины с дорогой связано с нежелательным трением. Но о каком трении может идти речь, если соприкасающиеся точки неподвижны? При внимательном изучении ближайшего к поверхности дороги участка шины видим, что:
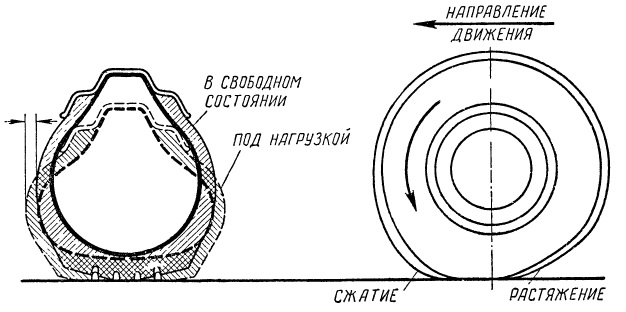
- шина сжимается, деформируется; происходит местное сжатие, а затем снова расширение шины; сжатие и расширение содержащегося в камере шины воздуха, взаимное перемещение частиц резины и частиц воздуха вызывает трение между ними;
- к точке контакта шины с дорогой все время подходят сжатые элементы шины, а от точки отрыва шины от дороги отходят, наоборот, растянутые; так как резина эластична и прочна, шина не разрывается, а только сжимается и растягивается в области контакта ее с дорогой, поэтому происходит некоторое скольжение отдельных частиц шины по поверхности дороги и, как следствие, трение;
- в углублениях поверхности дороги и рисунка протектора находится воздух; набегая на дорогу, участки протектора сплющиваются, резина заполняет углубления, выжимает из них воздух и как бы присасывается к поверхности дороги, и на отрыв шины от дороги требуется затрата дополнительной силы.
Рис. Работа колеса вызывает деформацию (изменение формы) шины.
Нетрудно сделать вывод, что описанные явления трения или сопротивления качению должны усиливаться при понижении давления в шине (так как при этом увеличиваются ее деформации) и при возрастании окружной скорости шины, а также при неровной или шероховатой поверхности дороги и при наличии заметных выступов и углублений в рисунке протектора шины.
Это на твердой дороге. А мягкую или не очень твердую дорогу, даже размягченный жарой асфальт, шина проминает и на это тоже приходится затрачивать часть тяговой силы.
Сопротивление качению колеса оценивается коэффициентом сопротивления качению f.
Коэффициент сопротивления качению равен отношению величины силы Pf, необходимой для качения колеса, к величине реакции Z:
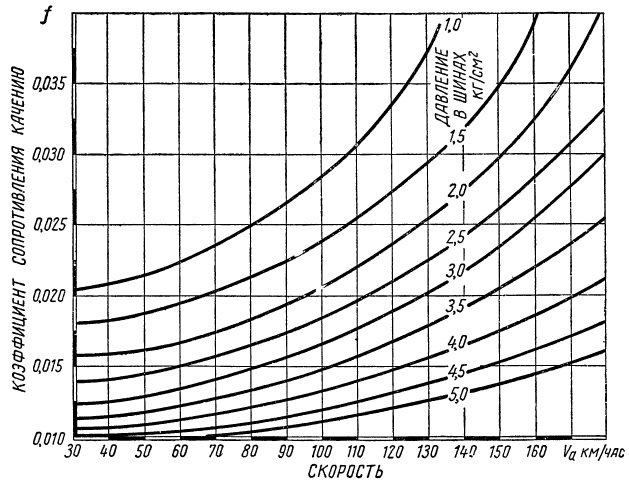
Величина коэффициента сопротивления качению f возрастает с уменьшением давления в шине, с увеличением скорости движения (при малых скоростях увеличение коэффициента f незначительно) и с увеличением неровности дороги. Изменение величины f ясно видно из рассмотрения графика зависимости коэффициента f от скорости движения и давления в шине (на асфальте). Ниже даны значения этого коэффициента для различных видов дорог для скорости 30—60 км/час и при давлении в шинах около 2,5 кг/см2.
| Коэффициент сопротивления качению | |
| Асфальт | 0,015 |
| Булыжник в хорошем состоянии | 0,018 |
| Былыжник в плохом состоянии | 0,023 |
| Брусчатая мостовая | 0,017 |
| Гравийное шоссе в хорошем состоянии | 0,022 |
| Гравийное шоссе в плохом состоянии | 0,028 |
| Ровная твердая проселочная дорога | 0,023 |
| Проселочная дорога среднего качества | 0,026 |
| Тяжелая проселочная дорога | 0,03 |
| Песок средней рыхлости | 0,15 |
| Снег утрамбованный | 0,029 |
Так как сопротивление качению находится в прямой зависимости от величины коэффициента можно установить, что если для движения автомобиля по асфальту требуется определенная сила, то для движения по булыжнику и по гравийному шоссе нужна в 1,5 раза большая сила, для движения по проселку — в 2 раза, по песку — в 10 раз.
Из уравнения следует, что сила сопротивления качению равна:
или, так как реакция Z равна нагрузке на колесо,
Подсчитав силы сопротивления качению для отдельных колес и сложив их, получаем силу сопротивления качению автомобиля. Хотя сопротивление качению передних, задних, левых и правых колес неодинаковое, без большой ошибки допустимо подсчитывать суммарную силу сопротивления качению для движения с определенной скоростью по уравнению:
где Ga — полный вес автомобиля в кг.
Рис. Коэффициент сопротивления качению увеличивается с возрастанием скорости и с понижением давления в шинах.
На преодоление сопротивления качению затрачивается энергия и нужно уметь вычислить расходуемую при этом мощность.
Прежде чем перейти к мощности, вспомним, что отрезок пути S, пройденный автомобилем в единицу времени t, называется скоростью движения:
Путь измеряют метрами или километрами, а время — секундами или часами; поэтому единицами измерения скорости будут либо метры в секунду (Vа м/сек), либо километры в час (Vа км/час), причем 1 м/сек = 3,6 км/час.
Мощность вычисляют как отношение работы (PS кгм) ко времени (t сек.); так как отношение пути ко времени выражает скорость, то мощность можно вычислить и как произведение силы на скорость:
Значит, чтобы узнать мощность Nf в л.с., расходуемую на сопротивление качению, нужно помножить силу сопротивления Pf на скорость движения va в м/сек и разделить на 75, так как 1 л. с. соответствует механической работе в 75 кгм в 1 сек. Если скорость V выражена в км/час, нужно умножить полученное уравнение мощности на 1000 (метров в километре) и разделить на 3600 (секунд в часе):
Для того чтобы автомобиль двигался, тяговая сила Рк на ведущих колесах должна быть меньше силы сцепления колес с грунтом (иначе колеса будут скользить, буксовать) и не меньше силы сопротивления движению, которую при езде по горизонтальной дороге с невысокой постоянной скоростью (когда сопротивление воздуха незначительно) можно считать равной силе сопротивления качению, иначе колеса не смогут вращаться и двигатель перестанет работать.
В зависимости от числа оборотов вала двигателя и от открытия дроссельной заслонки крутящий момент двигателя изменяется. Почти всегда можно сочетать различные значения момента двигателя и передаточных чисел в коробке передач таким образом, чтобы, как сказано выше, тяговая сила была меньше силы сцепления и не меньше силы сопротивления движению.
Для небыстрого движения по асфальту всем автомобилям требуется значительно меньшая сила тяги, чем они могут развить даже на высшей передаче, поэтому ехать нужно с прикрытой дроссельной заслонкой. Как говорят, автомобили в этом случае обладают большим запасом тяги.
На проселочной дороге дело несколько меняется. Легковые автомобили, если нет ухабов, могут ехать на высшей передаче, но при сильном нажатии на педаль подачи топлива. У грузовых автомобилей (с полной нагрузкой) разница между максимальной тяговой силой на высшей передаче и силой сопротивления качению на проселке очень невелика. Поэтому незначительное отклонение от скорости, соответствующей наибольшему крутящему моменту двигателя (40—32 км/час), вызывает необходимость включения следующей передачи (вспомним, что при уменьшении числа оборотов или подачи топлива крутящий момент уменьшается, а вместе с ним и тяговая сила).
Для движения легковых автомобилей по песку тяговой силы на прямой передаче вообще недостаточно, а на второй передаче движение возможно лишь с определенной скоростью (32—26 км/час) и при полной подаче топлива; практически нужно ехать на первой передаче. Автомобиль ГАЗ-51 способен идти по песку только на первой передаче, а ЗИЛ-150 — только на первой и второй передачах. Следует оговориться, что есть такие пески, по которым обычный автомобиль и на первой передаче проехать не может.
Сила сцепления на сухом асфальте больше тяговой силы на любой передаче у любого из рассматриваемых автомобилей. Но на мокром или обледенелом асфальте движение на пониженных передачах и трогание с места без буксования возможно на легковых автомобилях только при неполном открытии дроссельной заслонки, т. е. со сравнительно небольшим крутящим моментом двигателя; для грузовых автомобилей это относится к первой и второй передачам.
Источник статьи: http://ustroistvo-avtomobilya.ru/shiny-i-diski/koleso-i-doroga/