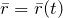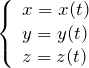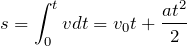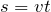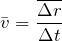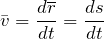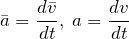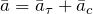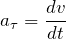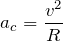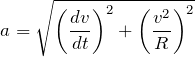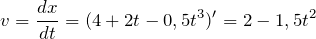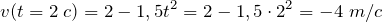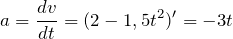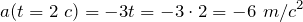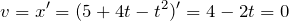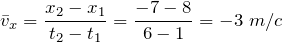Кинематическое уравнение движения автомобиля

Кинематические уравнения движения

Кинематические уравнения движения используются, чтобы описать перемещение объекта в пространстве. Так как при поступательном движении все точки объекта движутся одинаково, то его удобно представлять материальной точкой: она имеет определенную массу, однако её размерами можно пренебречь. Чтобы количественно описать движение точки, нужно ввести временную и пространственные координаты. При поступательном движении удобней всего пользоваться декартовой системой координат.

Положение такой точки в пространстве описывается радиус-вектором:

Можно спроектировать его на оси координат, тогда получим систему скалярных уравнений. Эти уравнения и называют кинематическими уравнениями движения:

Характеристики кинематического уравнения движения

Длина пути точки, пройденного ею с начального момента до момента t, обозначается и является скалярной величиной. Если движение прямолинейное, то вектор перемещения , соединяющий начальное и конечное положение точки, совпадает с путем точки, . Если же движение криволинейное, обычно находят с помощью геометрических построений.

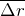
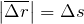
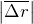
Длина пути, пройденная точкой за конечное время t, может быть найдена с помощью формулы:

Здесь v – функция изменения скорости точки во времени, 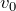— начальная скорость, а – ускорение, t – время.

Если движение равномерное, то есть скорость остается неизменной, пройденный путь можно найти проще:

Скорость – величина векторная; она характеризует не только быстроту движения точки, но и направление этого движения. Она направлена так же, как и вектор перемещения. Средняя скорость может быть рассчитана:

Если интервал времени 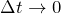, вектор перемещения стремится к тому, чтобы совпадать с путем перемещения, и тогда может быть вычислена мгновенная скорость:

Ускорение точки (в векторном или скалярном виде) мы узнаем, взяв производную от скорости по времени:

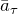
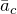
Если движение криволинейно, ускорение можно разложить на две составляющие: тангенциальное ускорение и центростремительное ускорение :

где R – это радиус кривизны рассматриваемой траектории. Модуль ускорения, включающего обе компоненты, при криволинейном движении:

Если движение имеет прямолинейный характер, ускорение имеет только тангенциальную составляющую.

Примеры решения задач

Задание	Задана материальная точка, которая перемещается вдоль оси абсцисс. Движение совершается по закону: х = 4 + 2t – 0,5t 3 . Для t = 2 c найдите координату этой точки, её мгновенные скорость и ускорение.
Решение	1) Найдём координату точки, воспользовавшись уравнением движения:

м.

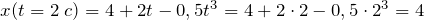
2) Вычислим производную от уравнения движения и найдём мгновенную скорость точки:

3) Вычислим производную от уравнения скорости, чтобы найти мгновенное ускорение:

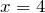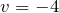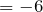Ответ В рассматриваемый момент времени м, м/с, м/с

Задание	Материальная точка движется по оси Х. Пусть её движение совершается по закону: х = 5 + 4t – t 2 . Нужно построить график функций, отображающих зависимость пути s и координаты х от времени. Найдите среднюю скорость, а также среднюю скорость пути за отрезок времени от t1 = 1 c до t2 = 6 с.
Решение	Чтобы построить требуемый график, найдём начальную и самую большую из достигнутых координаты, после чего найдем моменты времени, соответствующие этим координатам, а также координате х = 0.

В начальной координате объект находится в момент времени t = 0. Её значение:

х (t = 0) = 5 + 4t – t 2 = 5 + 4•0 – 0 2 = 5 м.

Из уравнения движения видим, что ускорение точки (заданное последним слагаемым) отрицательное. Значит, скорость уменьшается, и максимальная координата будет достигнута в тот момент, когда скорость начнёт менять знак. Найдём скорость как первую производную, взятую от уравнения движения, и приравняем ее к нулю:

Отсюда t = 2 c – момент, когда координата будет максимальной. Найдём эту координату:

х (t = 2) = 5 + 4t – t 2 = 5 + 4•2 – 2 2 = 9 м.

Найдём момент времени, когда координата х = 0:

х = 5 + 4t – t 2 = 0.

Решив это квадратное уравнение, получим корни: t₁ = 5 c, t₂ = -1 c. Последний результат отбрасываем, как нефизический.

Поскольку график, выражающий зависимость координаты от переменной времени, представляет собой кривую линию второго порядка, то в него входят пять разных коэффициентов. Поэтому найдём координаты еще для двух значений времени:

х (t = 1) = 5 + 4t – t 2 = 5 + 4•1 – 1 2 = 8 м.

х (t = 6) = 5 + 4t – t 2 = 5 + 4•6 – 6 2 = -7 м.

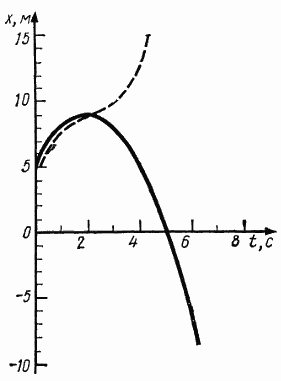
За этими данными мы можем начертить график для координаты. График пути строим за предыдущим графиком следующим образом:

1) До того, как скорость изменит свой знак, графики пути и координаты повторяют друг друга;

2) Начиная с момента, когда скорость изменит свой знак, путь возрастает по той же функции, по какой убывает координата.

Вычислим среднюю скорость за отрезок времени от t₁ = 1 c до t₂ = 6 с:

Чтобы найти среднюю путевую скорость, найдём путь, пройденный точкой за интервал времени от t₁ = 1 c до t₂ = 6 с. Этот путь складывается из двух отрезков пути – до и после перемены знака скорости:

Источник статьи: http://ru.solverbook.com/spravochnik/uravneniya-po-fizike/kinematicheskie-uravneniya-dvizheniya/

Уравнение движения автомобиля

Уравнение движения автомобиля выражает связь между движущими силами и силами сопротивления движению и позволяет определить режим движения автомобиля в любой момент.

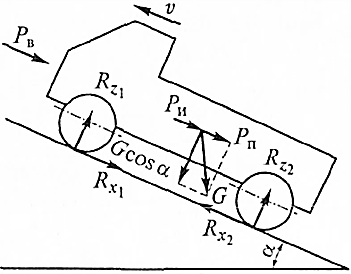
Для вывода уравнения движения используется схема движения автомобиля на подъем и рассматривается разгон автомобиля на подъеме (рис. 4.1).

Рисунок 4.1 – Схема сил, действующих на автомобиль на подъеме

Проекция всех сил, действующие на автомобиль на поверхность дороги:

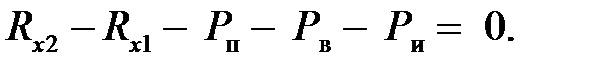(4.1)

Подставим в формулу (4.1) касательные реакции дороги R_х1 и R_х2, объединим члены с коэффициентом сопротивления качению f и члены с ускорением j и, принимая во внимание соотношения f (R_zl + R_z2) = P_к. При этом учтем, что j_k1 + j_k2 = j_k ,а также принимая во внимание коэффициент учета вращающихся масс, получим уравнение движения автомобиля в общем виде: .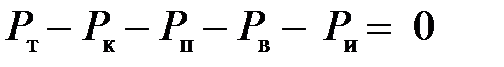

Принимая во внимание, что силы сопротивления качению Р_к и подъему Р_п в совокупности представляют силу сопротивления дороги Р_д, получим:

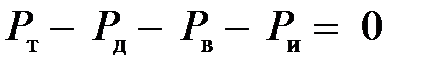(4.2)

При установившемся (равномерном) движении, когда нет разгона и Р_и = 0:

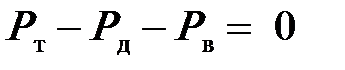(4.3)

Из уравнения (4.3) следует, что безостановочное движение автомобиля возможно только при условии:

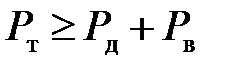(4.4)

Данное неравенство связывает конструктивные параметры автомобиля с эксплуатационными факторами, обусловливающими сопротивление движению, и не гарантирует отсутствия буксования ведущих колес. Безостановочное движение автомобиля без буксования ведущих колес возможно лишь при соблюдении условия:

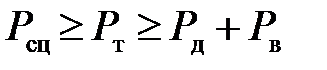(4.5)

Условие равномерного движения при отсутствии буксования ведущих колес записывается в виде:

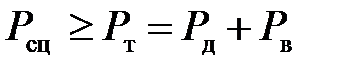(4.6)

|	следующая лекция ==>
Сила и мощность сопротивления разгону	|	Силовой баланс автомобиля

Дата добавления: 2017-06-02 ; просмотров: 2269 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ

Источник статьи: http://helpiks.org/9-18882.html

Кинематические уравнения движения

ВВЕДЕНИЕ

Основная задача физики – это установление устойчивых связей между физическими величинами, измеренных с помощью приборов в принятых единицах.

Для построения системы физических единиц произвольно выбирают единицы для нескольких не зависящих друг от друга физических величин. Эти единицы называются основными. Остальные же величины и их единицы выводятся из законов, связывающих эти величины и их единицы с основными. Они называются производными.

Мы будем использовать систему физических единиц интернациональную (система СИ).

В СИ выбраны семь величин (длина, масса, время, сила тока, температура, количество вещества, сила света) и для них установлены основные единицы измерения физических величин: метр, килограмм, секунда, ампер, кельвин, моль, кандела.

В механике мы будем использовать пять основных единиц:

Масса — килограмм (кг) — масса, равная массе международного прототипа килограмма (платиноиридиевого цилиндра, хранящегося в Международном бюро мер и весов в Севре, близ Парижа).

Длина пути — метр (м) — длина пути, проходимая светом в вакууме за 1/299792458 с.

Время — секунда (с) — время, равное 9.192 10 9 периодам излучения, возникающего между уровнями основного состояния атомов Cs-133 .

Радиан (рад) — угол между двумя радиусами окружности, длина дуги между которыми равна радиусу.

Стерадиан (ср) — телесный угол с вершиной в центре сферы, вырезающий на поверхности сферы площадь, равную площади квадрата со стороной, равной радиусу сферы.

Пример производной единицы измерения скорости: из формулы равномерного прямолинейного движения V = s / t единица скорости получается равной 1 м/с (здесь V — скорость, s — пройденный путь, t — время).

Используемые в физике величины бывают двух видов:

Скаляр — величина, характеризуемая числовым значением (она может быть положительной и отрицательной).

Вектор — величина, характеризуемая как числовым значением (модуль вектора, положительное число), так и направлением.

МЕХАНИКА

Механика — раздел физики, изучающий закономерности механического движения.

Механическое движение — это изменение с течением времени взаимного расположения тел или их частей.

Классическая механика (механика Ньютона) — изучает законы движения макроскопических тел, скорости которых малы по сравнению со скоростью света в вакууме (с ≈ 3 10 8 м/с).

Релятивистская механика — изучает законы движения макроскопических тел со скоростями, сравнимыми со скоростью света в вакууме.

Квантовая механика — изучает законы движения микроскопических тел (отдельных атомов, элементарных частиц)

Классическая механика делится на три раздела:

Кинематика — изучает движение тел, не рассматривая причины этого движения.

Динамика — изучает причины движения тел.

Статика — изучает законы равновесия системы тел.

КЛАССИЧЕСКАЯ МЕХАНИКА

Кинематика материальной точки

Материальная точка — тело, обладающее массой, размерами которого в данной задаче можно пренебречь.

Произвольное макроскопическое тело или систему тел можно условно разбить на малые части, каждая из которых рассматривается как материальная точка, а изучение произвольной системы сводится к изучению системы материальных точек.

Кинематические уравнения движения

Движение тела происходит в пространстве и во времени.

Положение материальной точки определяется в система отсчета — совокупность системы координат и часов.

Мы будем использовать декартову систему координат, в которой положение точки в данный момент времени задается тремя координатами x, y, z или радиусом-вектором , проведенным из начала системы координат в данную точку (см. рис. 1).

При движении материальной точки ее координаты с течением времени изменяются и ее движение определяется либо скалярными кинематическими уравнениями движения

либо векторными кинематическим уравнением движения .

Исключая в этих уравнений время, получим уравнение траектории — линии, описываемой материальной точкой в пространстве.

В зависимости от вида траектории различают прямолинейное и криволинейное движение.

Плоская траектория – если она располагается в одной плоскости.

Мы будем рассматривать только плоские траектории.

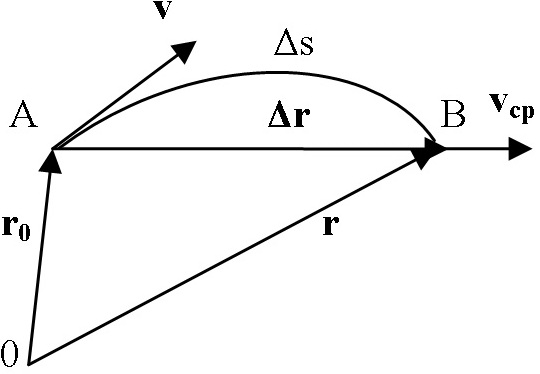
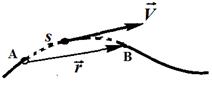
Длина пути s – это длина участка траектории, пройденного материальной точкой с момента начала движения (на рис. 2 она показана пунктиром), она является скалярной функцией времени s(t).

ds – бесконечно малый путь. Единица измерения пути [s, ds] = [м].

Перемещение — это вектор, проведенный из начального положения движущейся точки в положение ее в данный момент времени.

Модуль перемещения: | | = r, dr – бесконечно малое перемещение.

Единица измерения перемещения [r, dr] = [м]

При прямолинейном движении модуль перемещения r равен пройденному пути s.

1.2. Скорость

Скорость 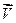— это векторная величина,характеризующая как быстроту движения, так и его направление в данный момент времени.

Мгновенная скорость (скорость в данный момент времени)

и вектор мгновенной скорости направлен по касательной к траектории в сторону движения (для прямолинейного движения вектора 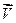и сонаправлены).

Модуль мгновенной скорости . Единица измерения скорости [V] = [м/с].

Для равномерного движения (V = const) V = s/t, где s – путь, пройденный за время t.

При неравномерном движении вводится скалярная величина — средняя скорость = Ds/Dt, где – длина пути, пройденного материальной точкой за время , s_i – длина пути, пройденного материальной точкой за время t _i

Правило сложения скоростей: если система отсчета 1, в которой движется тело с постоянной скоростью V₁, сама движется относительно системы отсчета 2 со скоростью V₂, то скорость тела относительно системы отсчета 2 равна векторной сумме векторов V₁ и V₂.

Ускорение

Ускорение — векторная величина, характеризующая быстроту изменения скорости по модулю и направлению. Мгновенное ускорение .

При ускоренном прямолинейном движении вектора скорости и ускорения сонаправлены, при замедленном прямолинейном движении эти вектора противонаправлены.

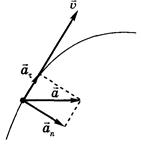
При криволинейном движении точки вектор ускорения отклонен от касательной к траектории в сторону ее вогнутости: при ускоренном движении угол между векторами скорости и ускорения острый, а при замедленном движении – тупой (рис. 3).

Модуль ускорения , единица измерения [a] = [м/с 2 ].

Для равноускоренного движения: ,

где V_о и V – скорости в начальный и конечный момент движения, t – время движения.

Для плоской траектории можно выделить два направления – касательную к траектории (орт ) и главную нормаль (орт ). Тогда вектор можно разложить на два вектора, направленных вдоль этих направлений:

Вектор называется тангенциальным (касательным) ускорением, он направлена по касательной к траектории (как и скорость) и характеризует быстроту изменения скорости по модулю. При ускоренном движении вектор сонаправлен с вектором скорости, а при замедленном движении эти векторы противонаправлены (рис. 4).

Вектор называется нормальным (центростремительным) ускорением, он направлена по нормали к траектории к центру кривизны траектории и характеризует быстроту изменения скорости по направлению , здесь r – радиус кривизны траектории (если траектория окружность, то r – радиус окружности). Естественно .

Правило сложения ускорений

Если тело движется с постоянным ускорением а₁ в системе отсчета 1, а система 1 движется с постоянной скоростью относительно системы 2, то ускорение тела относительно системы отсчета 2 равна а₁.

Виды движения

В зависимости от величин a _t и a_n может быть девять видов движения.

Наиболее важные виды движения:

1.4.1. Прямолинейное равномерное движение: a _t = 0, a_n = 0,

кинематическое уравнение движения s = Vt, V = s / t

s – путь, пройденный за время t.

1.4.2. Прямолинейное равноускоренное (равнозамедленное) движение: a = const, a_n= 0, кинематические уравнения движения

V = V _o ± at,

здесь V_o — скорость в начальный момент времени, V – скорость в момент времени t, s – пройденный путь, t – время движения.

1.4.3. Равномерное движение по окружности: a _t = 0, a_n = сonst

(хотя a_n = сonst, но направление вектора изменяется, т.е. это ускоренное движение).

Угловая скорость есть векторная величина, модуль которой (здесь d j — бесконечно малый угол поворота материальной точки за бесконечно малый промежуток времени dt).

Вектор направлен вдоль оси вращения по правилу правого винта (рис. 5).

Единица измерения угловой скорости [ω] = [рад/с] .

Период вращения Т – время одного полного оборота.

Частота вращения ν – число оборотов за 1 секунду, единица измерения частоты [ν, ω] =[c -1 ] = [Гц].

Имеет место соотношения: .

Для равномерного движения по окружности w = const

и кинематическое уравнение j = wt.

1.4.4. Равноускоренное движение по окружности: a _t = const, a_n = сonst;

Угловое ускорение − векторная величина, модуль которой ,

причем вектор углового ускорения cонаправлен вектору угловой скорости при ускоренном движении и противонаправлен ему при замедленном движении (рис. 6).

Единица измерения [ε] = [рад/с 2 ].

Кинематические уравнения равнопеременного движения по окружности: ω = ω_o ± εt, ,

где w_o — начальная угловая скорость.

Связь между линейными и угловыми величинами:

1.5. Тело, брошенное под углом α к горизонту с начальной скоростью V_o [Для самостоятельной работы]

;

,

,

в точке падения скорость тела равна по абсолютной величине скорости тела в точке бросания, а направле­ние ее составляет тот же угол, что и в точке бросания (взятый с противоположным знаком);

время подъема (= времени падения) , ,

, .

Тело, брошенное горизонтально, будет двигаться по одной из ветвей параболы с вершиной в точке бросания.

Дата добавления: 2019-02-26 ; просмотров: 1500 ; Мы поможем в написании вашей работы!

Источник статьи: http://studopedia.net/13_49916_kinematicheskie-uravneniya-dvizheniya.html