Лекции по динамике автомобиля

Устройство автомобилей

Основы динамики автомобиля

Скоростная характеристика двигателя

Скоростная характеристика двигателя определяется зависимостями эффективной мощности N_e и крутящего момента M_к от частоты вращения n коленчатого вала.

Ведущие колеса автомобиля приводят его в движение в результате возникновения силы тяги, которая возникает при приложении крутящего момента к полуосям ведущих колес со стороны трансмиссии:

где P_т – сила тяги, Н;
M_т – крутящий (тяговый) момент на ведущем колесе, Нм;
r – радиус колеса, м.

Крутящий момент на ведущих колесах зависит от величины момента, развиваемого двигателем на коленчатом валу, передаточного числа i_тр трансмиссии и ее КПД – η_тр :

Сила тяги P_т на ведущих колесах может быть определена не только по формуле (1), но и с учетом скорости v_i движения автомобиля на i -й передаче и развиваемой двигателем эффективной мощности N_е :

Скорость v_i движения автомобиля на i -й передаче пропорциональна частоте n вращения коленчатого вала, радиусу r ведущего колеса и обратно пропорциональна передаточному числу i_тр i трансмиссии на i -й передаче:

Таким образом, частота вращения n коленчатого вала является определяющим параметром для показателей эффективной мощности N_е , крутящего момента M_к и силы тяги на ведущих колесах P_т .

На рисунке 1 приведена внешняя скоростная характеристика двигателя при полностью открытой дроссельной заслонке, которая определяет предельные возможности двигателя при значениях частоты вращения коленчатого вала от n_min до n_max .

Анализ графика показывает, что максимальная эффективная мощность и максимальный крутящий момент, развиваемый двигателем, доступен в узком интервале частот вращения коленчатого вала. При небольшой частоте вращения коленчатого вала величина этих динамических показателей недостаточна для появления на ведущих колесах требуемой для движения автомобиля силы тяги, а при превышении частотой вращения коленвала некоторого максимального порога двигатель начинает терять мощность и тяговые показатели, или, как говорят механики, начинает работать «вразнос».
По этой причине эффективная эксплуатация двигателя внутреннего сгорания возможна лишь в некотором узком диапазоне частот вращения коленчатого вала.

Скоростная характеристика двигателя во многом зависит от типа двигателя: чем круче кривая эффективной мощности N_е , тем большей приемистостью обладает двигатель.

Тяговая характеристика автомобиля

Тягово-скоростные свойства автомобиля удобно оценивать с помощью тяговой характеристики, т. е. зависимостью силы тяги на ведущих колесах от скорости движения на различных передачах (рис. 2).

Используя скоростную характеристику и задавая частоты вращения коленчатого вала от n_min до n_max при соответствующих значениях эффективной мощности или крутящего момента для каждой передачи по формуле (4) находят значения скорости v , а по формуле (3) находят значение тяговой силы P_т .

Число кривых на тяговой характеристике (рис. 2) соответствует числу ступеней в коробке передач.

Тяговая характеристика позволяет быстро определить максимальное значение силы тяги на ведущих колесах, которая может быть обеспечена при данной скорости движения автомобиля, поскольку она рассчитывается по наибольшей для данной частоты вращения коленчатого вала мощности двигателя. Меньшее значение силы тяги получается при недоиспользовании мощности двигателя, т. е. при неполной подаче топлива. Следовательно, с помощью тяговой характеристики можно оценить предельные тяговые возможности автомобиля в фактическом интервале скоростей его движения.

Силы и моменты, действующие на ведущие колеса

На ведущие колеса автомобиля действуют силы со стороны автомобиля (т. е. со стороны двигателя посредством агрегатов трансмиссии), а также силы со стороны дороги. Обозначим силы, действующие со стороны автомобиля, буквой Р , а со стороны дороги – буквой R (рис. 3).

Реактивные силы, действующие на колеса

Тяговый момент М_т на ведущих колесах стремится сдвинуть назад верхний слой дорожного покрытия, в результате чего со стороны дороги на ведущее колесо в зоне контакта действует противоположно направленная сила R_x – горизонтально направленная касательная реакция дороги.

Так как на автомобиле используются эластичные пневматические шины, то неизбежна частичная потеря момента М_т , поэтому продольную (горизонтальную) реакцию со стороны дороги, обеспечивающую качение колеса, можно записать как разность между силой тяги и потерями в шине:

где Р_ш – сила, учитывающая потери энергии в шинах ведущих колес.

Таким образом, касательная реакция дороги создает силу тяги.

Автомобиль своим весом G действует на каждое колесо, передавая усилие на дорогу, и, соответственно, вызывая нормальную реакцию дороги R_z . Следует учитывать, что при наличии на колесе крутящего момента нормальная реакция R_z прикладывается не к оси симметрии опорной площадки колеса, а на некотором расстоянии α_ш от нее, поскольку имеет место смещение центра давления из-за эластичности шины.

Эпюра элементарных нормальных реакций дороги, показанная на рисунке 4, объясняет причину смещения точки приложения реакции R_z . Это происходит из-за того, что нормальные реакции на переднем и заднем участках опорной площадки колеса различны по величине, так как силы, возникающие в упругом материале шины при приложении и снятии нагрузки неодинаковы.
Это объясняется действием сил внутреннего трения между взаимно перемещающимися частицами материала шины. При приложении нагрузки эти силы и силы упругости направлены в одну и ту же сторону, а при снятии – в противоположные стороны.

Боковая сила Р_y значительно увеличивается при криволинейном движении автомобиля или при движении по косогору. Боковая реакция R_y со стороны дороги удерживает колеса автомобиля от бокового скольжения (заноса) при движении автомобиля поперек косогора или при выполнении маневра.

Сила тяги на ведущих колесах

Сила тяги Р_т на ведущих колесах может быть определена, как отношение крутящего (тягового) момента M_т , подводимого к колесам, к их радиусу r :

При этом не учитываются затраты энергии на деформацию дорожного покрытия, трение внутри шины и силы инерции, обусловленные ускорением вращающихся масс колес и деталей трансмиссии в случае неравномерного движения.

Следует учитывать, что радиус колеса вследствие эластичности шины является переменной величиной.
Различают следующие радиусы автомобильных колес:

• статический радиус колеса r_ст – расстояние от поверхности дороги до оси неподвижного колеса, воспринимающего вертикальную нагрузку, обусловленную силой тяжести, действующей на автомобиль (т. е. его весом G ). Значения статического радиуса приводятся заводом-изготовителем шины в технических характеристиках;
• динамический радиус колеса r_д – расстояние от поверхности дороги до оси катящегося колеса. Динамический радиус колеса во время движения может превышать его статический радиус, поскольку в результате нагрева шины давление внутри нее увеличивается.
  Кроме того, под действием центробежных сил с возрастанием скорости автомобиля шина растягивается в радиальном направлении, вследствие чего динамический радиус увеличивается. Динамический радиус, также, зависит от величины вертикальной нагрузки P_z .
• радиус качения колеса r_к – радиус условного недеформирующегося катящегося без скольжения колеса, которое имеет с данным эластичным колесом одинаковую угловую и линейную скорости.

Радиус качения колеса определяется по формуле:

где S – путь, пройденный колесом; n_к – число оборотов колеса на пути S .

Если проскальзывание колеса относительно дороги отсутствует, что характерно для ведомого колеса, то радиусы r_д и r_к почти равны между собой. В случае полного буксования колеса его пройденный путь будет равен нулю, и тогда (согласно приведенной выше формуле) его радиус качения тоже будет равен нулю.
В случае движения колеса юзом (скольжение без вращения) число оборотов будет равно нулю, и, соответственно, радиус качения r_к будет стремиться к бесконечности.

Различают еще и свободный радиус колеса r_св , который является половиной диаметра ненагруженного колеса при отсутствии его контакта с опорной поверхностью.

На дорогах с сухим покрытием скольжение ведущих колес и изменение радиуса незначительны. Поэтому радиусы статический r_ст , динамический r_д и качения r_к при расчетах считаются одинаковыми и обозначаются буквой r .

Источник статьи: http://k-a-t.ru/PM.01_mdk.01.01/7_teoria_avto_3/index.shtml

Динамика автомобиля — Vehicle dynamics

Для транспортных средств, таких как автомобили, динамика транспортного средства — это исследование того, как транспортное средство будет реагировать на действия водителя на заданной твердой поверхности.

Динамика транспортных средств — это часть инженерной мысли, в основе которой лежит классическая механика .

Содержание

Факторы, влияющие на динамику автомобиля

Аспекты конструкции автомобиля, влияющие на динамику, можно сгруппировать в трансмиссию и торможение, подвеску и рулевое управление, распределение массы, аэродинамику и шины.

Трансмиссия и торможение

• Компоновка автомобиля (т.е. расположение двигателя и ведущих колес)
• Трансмиссия
• Система торможения

Подвеска и рулевое управление

Некоторые атрибуты относятся к геометрии части подвески , рулевого управления и шасси . К ним относятся:

Распределение массы

Некоторые атрибуты или аспекты динамики автомобиля обусловлены исключительно массой и ее распределением. К ним относятся:

Аэродинамика

Некоторые атрибуты или аспекты динамики автомобиля являются чисто аэродинамическими . К ним относятся:

Некоторые атрибуты или аспекты динамики автомобиля можно напрямую отнести к шинам . К ним относятся:

Поведение автомобиля

Некоторые атрибуты или аспекты динамики автомобиля являются чисто динамическими . К ним относятся:

Анализ и моделирование

Динамическое поведение транспортных средств можно анализировать несколькими способами. Это может быть как простая система пружинных масс , через модель велосипеда с тремя степенями свободы (DoF), так и с большой степенью сложности с использованием пакета моделирования многотельной системы , такого как MSC ADAMS или Modelica . Поскольку компьютеры стали быстрее, а программные пользовательские интерфейсы улучшились, коммерческие пакеты, такие как CarSim , стали широко использоваться в промышленности для быстрой оценки сотен тестовых условий намного быстрее, чем в реальном времени. Модели транспортных средств часто моделируются с помощью усовершенствованных конструкций контроллеров, предоставляемых в виде программного обеспечения в контуре (SIL) с программным обеспечением для проектирования контроллеров, таким как Simulink , или с физическим оборудованием в контуре (HIL).

Движение транспортного средства в значительной степени обусловлено поперечными силами, возникающими между шинами и дорогой, поэтому модель шины является важной частью математической модели. Модель шины должна создавать реалистичные поперечные силы во время торможения, ускорения, прохождения поворотов и их комбинаций при различных условиях поверхности. Используется много моделей. Большинство из них являются полуэмпирическими, как, например, модель волшебной формулы Пацейки .

Гоночные автомобильные игры или симуляторы также являются формой моделирования динамики транспортного средства. В ранних версиях было необходимо много упрощений, чтобы получить производительность в реальном времени с разумной графикой. Тем не менее, повышение скорости компьютера сочетается с интересом к реалистичной физике, что привело к созданию симуляторов вождения , которые используются в автомобильной инженерии с использованием подробных моделей, таких как CarSim .

Важно, чтобы модели соответствовали результатам испытаний в реальном мире, поэтому многие из следующих испытаний коррелируют с результатами, полученными на оборудованных испытательных автомобилях.

Источник статьи: http://ru.qaz.wiki/wiki/Vehicle_dynamics

Автомобильный справочник

для настоящих любителей техники

Динамика автомобиля

Под динамикой автомобиля понимают его свойство перевозить грузы и пассажиров с максимально возможной средней скоростью при заданных дорожных условиях. Чем лучше динамика автомобиля, тем выше его производительность. Кроме того, динамика автомобиля в полной мере определяет безопасность его эксплуатации. Динамика автомобиля зависит от его тяговых и тормозных свойств.

Динамика прямолинейного движения

Общее сопротивление движению

Сопротивление движению вычисляется как (рис. «Силы сопротивления движению» ):

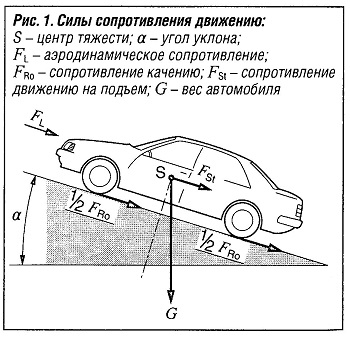
Мощность, которая должна поступить на ве­дущие колеса автомобиля для преодоления сопротивления движению (силы сопротивле­ния движению), равна:

P_W = F_W v или P_W = F_WV /3600

Сопротивление качению

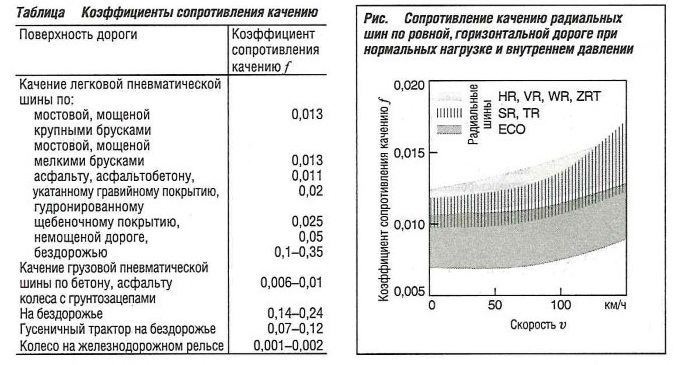
Сопротивление качению является следствием возникающих процес­сов деформации в зоне контакта шины с до­рогой. При этом применимо следующее:

Fro =f G cosa — fmg cosa

Приближенный расчет сопротивления каче­нию может быть выполнен путем использо­вания коэффициентов, представленных в приведенной ниже таблице «Коэффициенты сопротивления качению» и на рис. «Сопротивление качению радиальных шин по ровной, горизонтальной дороге при нормальных нагрузке и внутреннем давлении».

Увеличение коэффициента сопротивления качению f прямо пропорционально уровню деформации и обратно пропорционально ра­диусу шины. Следовательно, коэффициент будет увеличиваться при увеличении нагрузки, скорости и при снижении давления в шине.

При прохождении поворотов сопротивле­ние качению увеличивается за счет добавоч­ного сопротивления повороту:

F_k=f_кG

Коэффициент сопротивления повороту f_к является функцией скорости движения авто­мобиля, радиуса поворота, геометрических характеристик подвески автомобиля, типа шин, давления в шинах и поведения автомо­биля под действием поперечного ускорения.

Таблица.«Коэффициент аэродинамического сопротивления и мощность, затрачиваемая на преодоление аэродинамического сопротивления, для различных типов кузова»

Аэродинамическое сопротивление

Определяется по формуле:

F_L = 0,5 p⋅ c_w⋅ А (v + v₀) 2

F_L =0,0386⋅ р⋅ c_w⋅ А (v + v₀) 2 ,

где: v в км/ч, F_L в Н, р в кг/м 3 , А в м 2 , плотность воздуха р = 1,202 кг/м 3 на высоте 200 м.

P_L = F_L = 0,5 р c_w Av (v + v₀) 2

P_L = 12,9-10 -6 c_w A v (v + v₀) 2

Максимальное поперечное сечение автомобиля: А ≈0,9 х ширина колеи х высота.

Эмпирическое определение коэффициентов аэродинамического сопротивления и сопротивления качению

Автомобиль движется накатом на нейтральной передаче в условиях безветрия по ровной до­роге. Для двух заданных значений скоростей движения, v₁ (высокая скорость) и v₂ (малая скорость), замеряется время, необходимое, чтобы автомобиль при этих условиях замед­лил свое движение. Эта информация исполь­зуется для расчета средних замедлений a₁ и а₂. Формулы и примеры из табл. «Эмпирические определения коэффициентов аэродинамического сопротивления и сопротивления качению» приведены для автомобиля массой m = 1450 кг с площадью поперечного сечения А = 2,2 м 2 .

Этот метод применим для скоростей дви­жения автомобиля до 100 км/ч.

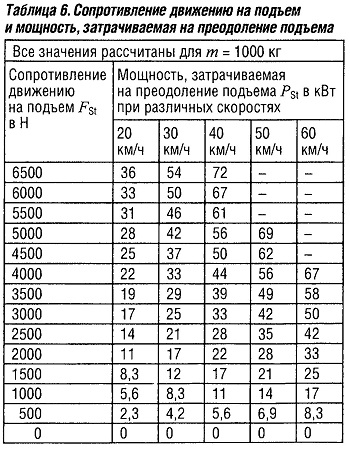
Сопротивление движению автомобиля на подъем и силы, действующие на автомобиль при движении под уклон

Сопротивление движению на подъем (F_st со знаком плюс) и силы, действующие на автомо­биль при движении под уклон (F_st со знаком минус) рассчитываются следующим образом:

F_st = G sinа = m g sina

F_st ≈ 0,01 m g p

Эти уравнения применимы с уклонами до р ⩽ 20%, поскольку при малых углах применимо следующее:

sina ≈ tana (погрешность менее 2 %).

Мощность, затрачиваемая на преодоление подъема, равна:

P_st = F_st v или если P_st измеряется в кВт, F_st в Н и v в км/ч:

P_st = F_st v/3600 = m g v sina/3600

_Pst = m g p v / 3600

Продольный уклон дороги равен:

р = (h/l)⋅100 % или р = (tanа) ⋅100 %

где h соответствует проекции наклонной поверхности l на вертикальную ось.

В англоязычных странах продольный уклон определяется отношением 1 в 100/р .

Например, при р =50% отношение 1 к 2.

Пример вычисления силы тяги и мощности, затрачиваемой на преодоление подъема

Для преодоления подъема с уклоном р = 21 %, автомобилю массой 1500 кг потре­буется сила тяги на колесах приблизительно 1,5 x 2000 Н = 3000 Н (значение из табл. «Угол уклона и сопротивление движению на подъем» ) и при v = 40 км/ч мощность, затрачиваемая на преодоление подъема, приблизительно 1,5 х 22 кВт = 31 кВт (значение из табл. «Сопротивление движению на подъем и мощность, затрачиваемая на преодоление подъема» ).

Сила тяги

Чем больше крутящий момент двигателя М и общее передаточное число трансмиссии i между двигателем и ведущими колесами, и чем ниже потери мощности в трансмиссии, тем выше сила тяги F на ведущих колесах автомобиля.

F = (Mi/r)⋅η или F = P η / v

η — КПД привода. Для двигателя про­дольного расположения η ≈ 0,88 — 0,92, для двигателя поперечного расположения η ≈ 0,91 -0,95.

Сила тяги частично затрачивается на преодо­ление сопротивления движению. При боль­шом сопротивлении движению, имеющем место на подъемах, следует включать в ко­робке передач пониженную передачу (т. е. увеличивать передаточное число трансмис­сии).

Частота вращения коленчатого вала двигателя и скорость автомобиля

Частота вращения коленчатого вала вычисляется как:

n = 60vi / 2 πr

или при v в км/ч:

n = 1000vi / 2π·60r

Ускорение

Избыточная сила F-F_w вызывает ускорение автомобиля. Или замедление, когда Fw превышает F

a = (F-Fw) / k_m m

a = (P η — P_w) / v k_m m

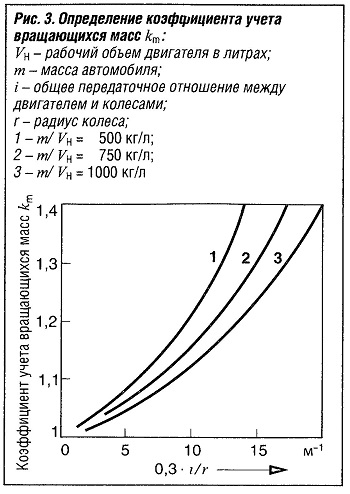
Коэффициент учета вращающихся масс k_m (рис. «Определение коэффициента учета вращающихся масс k_m» ) позволяет учесть дополнительное увеличение инерционных масс автомобиля из-за наличия вращающихся частей (колеса, маховик, коленчатый вал и т. п.).

Сила тяги и скорость автомобилей с автоматической трансмиссией

Когда уравнение силы тяги применяется для автомобилей с автоматической трансмиссией с гидротрансформатором или гидромуфтой, крутящий момент двигателя заменяется крутящим моментом турбины гидротранс­форматора, а частота вращения коленча­того вала двигателя — частотой вращения турбины гидротрансформатора. Используя кривую характеристики гидротрансформа­тора, можно определить зависимость между

и скоростной характеристи­кой двигателя

Силовой баланс для отдельных передач в функции скорости движения может быть определена из диаграммы силы тяги/сопротивления движению. На диаграмме можно увидеть точки излома, типичные для гидротрансформатора, возникающие вслед­ствие мультипликации крутящего момента. Максимальную скорость в каждом случае для данной передачи можно определить по точкам пересечения линий тягового усилия с линиями сопротивления движению.

Источник статьи: http://press.ocenin.ru/dinamika-avtomobilya/