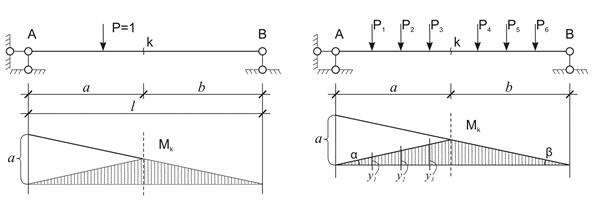
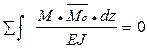Понятие линии влияния. Использование линии влияния при расчете сооружений на подвижные нагрузки.
Линия влияния – это график, показывающий зависимость определяемой величины от положения на сооружении единичного подвижного груза постоянного направления.
Р – передвигающийся по всей балке единичный безразмерный груз .
Необходимо найти положение подвижной нагрузки, при котором определенное усилие имеет экстремальное значение — опасное.
Линии влияния строятся двумя способами статическим и кинематическим.
При статическом методе используется статика, метод сечений. При построении линий влияния внутренних сил рассматривается положение груза слева и справа от расчетного сечения, соответственно получаем левые и правые линии влияния.
Сущность кинематического метода:
— отображается та связь, усилие в которой определяется. Получили механизм;
— взамен отброшенной связи прикладывается искомое усилие положительного направления;
— полученному механизму даем возможные перемещения в направлении искомого усилия;
— применяется принцип возможных перемещений: сумма работ всех действующих сил возможных перемещений равно нулю.
Определение усилий по линии влияния и заданной постоянной нагрузке.
1. Действие сосредоточенных сил Р.
Sк – определяемое усилие (R, Q, M); yi – величина усилия Sк, когда единичный груз находится в сечении действия силы Рi.
Sк =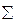 
Pi*yi
2. Действие распределенной нагрузки q.
Sк = q*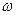 
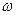
, где площадь линии влияния на участке действия равномерно распределенной нагрузки.
3. Действие сосредоточенного момента
Sк = М*tg 
где 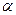– угол наклона линии влияния в том месте, где приложен момент и угол считается положительным при отсчете его от оси X до линии влияния против хода часовой стрелки.
Момент положителен по ходу часовой стрелки.
При одновременном действии всех нагрузок используется принцип независимости сил, все формулы объединяются:
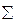
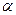
Sк = Pi*yi+ q* + М*tg .
6.Понятие ферм, признаки их статической неопределимости, определимости, основные способы определения усилий в стержнях ферм.
Расчёт плоских ферм.
Ферма- стержневая система, у которой во всех узлах шарнирыи при этом она остаётся геометрически неизменяемой.
Степень статической неопределимости ферм : n=C+Cо-2У,
где У-число узлов фермы.С-число стержней. Со-число опорных стержней.
Определение степени свободы для ферм:W=2У-С-Со.
Основные способы определения усилий в стержнях ферм:
1)Способ моментных точек
3)Способ вырезания узлов
Если невомзожен 1 способ то использ-ся 2,если же 2 способ неприменим , то используется 3 способ.
-способ моментных точек:
СуммаМк1=-N1*r1-Ra*d+P1*d/2=0,отсюда находим N1.
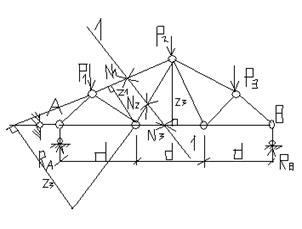
-способ проекций(моментные точки в бесконечности)
Статически неопределимые стержневые системы, определение степени статической неопр-ти, св-ва статически неопределимых систем. Сущность метода сил. Основные способы проверки правильности построения эпюр.
Стержневые системы — системы, состоящие из отдельных , обычно прямолинейных, соединенных между собой в узлах с помощью сварки, заклепок, болтов и других скреплений; одним из таких видов систем являются плоские фермы.
При расчете статически неопределимых рам определяют реакции опорных связей и внутренних усилий. Они принимаются за неизвестные. Если уравнений статики недостаточно для определения этих неизвестных, то система статически неопределима.
Свойства стат. неопределимых систем:
— распределение усилий между элементами зависит от материала этих элементов и их размеров;
— изменение температуры, смещение опорных связей, неточность изготовления элементов и последующей сборки все это приводит к появлению дополнительных усилий и напряжений.
Расчет статически неопределимых систем начинают с определения статической неопределимости – это число лишних связей, удаление которых превращает заданную стат. неопределимую раму в стат. определимую и геометрически неизменяемую.
Для рам степень статической неопределимости:
n=3m – Ш , Ш – число простых шарниров (соединяет 2 стержня или 2 диска);
m – число замкнутых контуров в системе в предположении отсутствия шарнирных соединений;
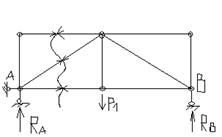
Задана стат. неопределимая рама. n=3*2 – 3 = 3 раза стат. неопределима.
Раскрытие статической неопределимости любой рамы методом сил начинается с отбрасывания дополнительных связей. Система, освобожденная от дополнительных связей, становится статически определимой. Она носит название основной системы.
Основная система метода сил – это статически определимая и геометрически неизменяемая система, полученная из заданной системы удалением лишних связей.
После того как дополнительные связи отброшены и система превращена в статически определимую, необходимо ввести вместо связей неизвестные силовые факторы. В тех сечениях, где запрещены линейные перемещения, вводятся силы. Там, где запрещены угловые смещения, вводятся моменты. Как в том, так и в другом случае неизвестные силовые факторы обозначают Xi-, где i — номер неизвестного. Наибольшее значение i равно степени статической неопределимости системы. Заметим, что для внутренних связей силы Xi, — являются взаимными. Если в каком-либо сечении рама разрезана, то равные и противоположные друг другу силы и моменты прикладываются как к правой, так и к левой частям системы.
Эквивалентная система – это основная система, загруженная реакциями отброшенных связей и заданной нагрузкой. Она д. б. тождественна заданной раме статически (внутр. силы одинаковы) и кинематически (перемещение точек д. б. одинаковыми)
Теперь составим уравнения совместности перемещений:
1(x1,x2,x3,х4,Р)=0
2(x1,x2,x3,х4,Р)=0 – первый индекс направление перемещения, второй – причина перемещения
3(x1,x2,x3,х4,Р)=0
4(x1,x2,x3,х4,Р)=0
Применяем принцип независимости сил и их сложения:
1(x1,x2,x3,х4,Р)= 1(x1)+ 1(x2)+ 1(x3) + 1(x4) + 1(Р)=0
1(x1)= 
11*x1 – принцип пропорциональности, где 11 – перемещение по направлению x1, от действия x1=1; 1(x2)= 12*x2 и т. д.
Записываем канонические уравнения метода сил. Число уравнений равно степени статич. неопределимости. Каждое уравнение это отрицание перемещений по направлению отброшенных связей.
11 x1+ 12 x2+ 13 x3+ 14 x4+ 1(Р)=0 – канн. ур., отрицание перемещ. по направл. x1.
21 x1+ 22 x2+ 23 x3+ 24 x4+ 2(Р)=0
31 x1+ 32 x2+ 33 x3+ 34 x4+ 3(Р)=0
41 x1+ 42 x2+ 43 x3+ 44 x4+ 4(Р)=0
Далее решаем каноническое уравнение. Для этого основную систему загружаем по отдельности единичными неизвестными по отдельности и строим эпюра единичных изгибаемых моментов. Находим коэффициенты при неизвестных:
ik= 
; i(Р)= 
Строим эпюру изгибающих моментов для заданной рамы:
М=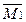 
Х1+ 
Х2+ 
Х3+ 
Х4+Мр
Способы проверки. Окончательная эпюра моментов проверяется дважды статически (явл. необходимой, но недостаточной) и кинематически.
Статическая – любой узел рамы должен находиться в равновесии, т. е. сумма моментов любого узла =0.
Кинематическая – проверяется отсутствие перемещений по направлению неизвестных (отброшенных связей). Сколько неизвестных столько и проверок:
1= 
; 2= 
Можно сделать суммарную проверку, т.е. отсутствие перемещений по направлению сразу всех неизвестных:
=М1+ М1+ М2+ М3; 
= 
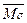
Источник статьи: http://infopedia.su/8xcf2.html