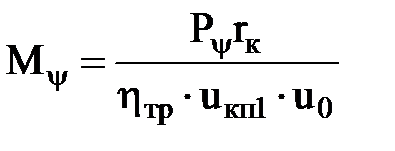Основы расчета типовых элементов фрикционных сцеплений



Расчет ведомого диска. Задачей расчета является определение радиусов фрикционных накладок, влияющих на размеры других элементов сцепления; определение необходимого усилия, от которого зависят число и характеристика нажимных пружин, сила, прикладываемая к педали сцепления, и передаточное число привода управления.
В нейтральном положении привода сцепление постоянно включено, а передаваемый им крутящий момент ограничивается моментом трения
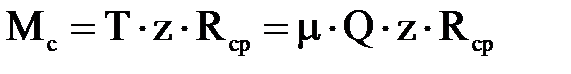
где Т – окружная сила трения, действующая между одной парой трущихся поверхностей, кН;
z – число пар поверхностей трения;
Rср – плечо силы Т, м;
μ – коэффициент трения (μ = 0,3…0,35);
Q – суммарная сила, создаваемая нажимными пружинами;
где Rн и Rв – соответственно наружный и внутренний радиусы кольцевой фрикционной накладки ведомого диска, м.
Чтобы сцепление во включенном состоянии не пробуксовывало, максимальный момент трения в нем Мс должен в β раз превышать максимальный крутящий момент двигателя Ме max .Следовательно, суммарная сила
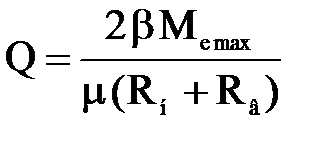
где β – коэффициент запаса сцепления.
Интенсивность изнашивания фрикционных накладок зависит от величины нагрузки на поверхности накладок. Чем она ниже, тем выше износостойкость фрикционных накладок. Поэтому нажимное усилие пружин
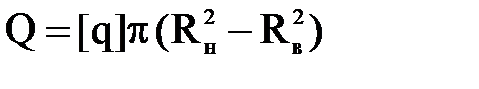
ограничивается допустимым давлением [q], и, задаваясь отношением Rв/ Rн = 0,55…0,70 и решая совместно (6.3) и (6.4), находят радиусы, а затем суммарную силу упругости нажимных пружин. При этом принимают для легковых автомобилей β = 1,2…1,75; для грузовых β = 1,5…3,0;
Другим параметром, определяющим износостойкость фрикционных накладок и тепловыделение в сцеплении, является удельная работа трения (буксования) Lуд. Поэтому основные размеры фрикционных накладок согласуют с условием
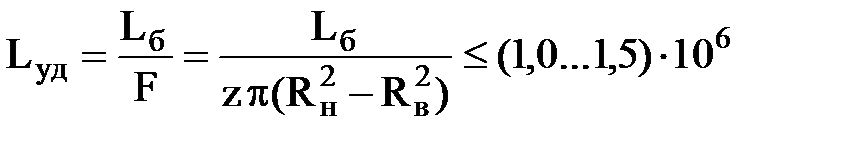
где Lб – работа буксования сцепления при одном трогании автомобиля с места на первой передаче при расчетном значении ψ = 0,02 или 0,16;
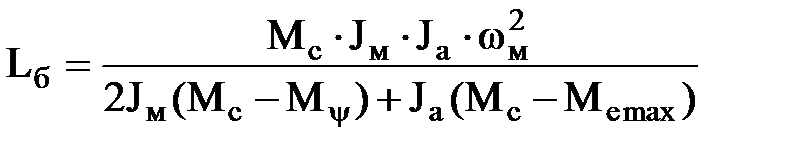
где Jм – момент инерции маховика и приведенных к нему деталей двигателя, Н·м 2 ;
Jа – момент инерции массы mа автомобиля, приведенный к ведомому диску сцепления, Н·м 2 ; определяется по выражению
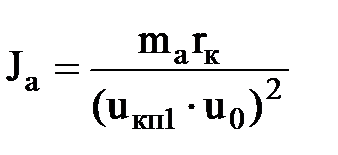
ωм – угловая скорость маховика, соответствующая максимальному крутящему моменту двигателя, с -1 ;
Мψ – момент сопротивления дороги, приведенный к ведомому диску сцепления, кН∙м;
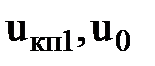
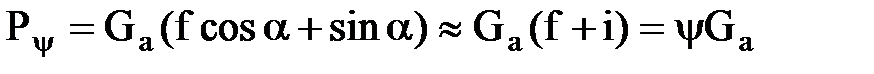
rк – радиус качения колеса, м.
Шлицевое соединение ступицы ведомого диска с первичным валом коробки передач рассчитывают по допустимому напряжению смятия:
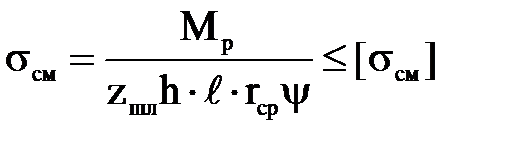
где Мр – расчетный момент; Мр = Ме max , кН∙м;
zшл – число шлицев;
h и ℓ – высота и длина поверхности контакта зубьев, м;
rср – средний радиус поверхности контакта зубьев, м;
ψ – коэффициент, учитывающий неравномерное распределение нагрузки по зубьям; ψ = 0,7…0,8;
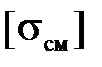
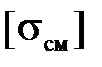
Для шлицев эвольвентного профиля h = m, rср = 0,5·m·zшл;
Для шлицев прямоугольного профиля h ≈ 0,5(D – d), rср = 0,25(D + d), — где m – модуль зуба; D и d – соответственно наружный и внутренний диаметры соединения.
Расчет нажимного диска. Нажимной диск является «тепловой губкой», поглощающей тепло, выделяемое при буксовании сцепления. Поэтому его делают массивным, обладающим необходимой теплоемкостью, жесткостью и прочностью. Массу mнд диска определяют из условия допустимого нагрева при трогании автомобиля с места:
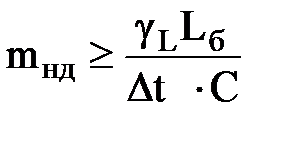
где γL – коэффициент, учитывающий, какая часть работы буксования Lб воспринимается рассчитываемой деталью (для нажимного диска однодискового сцепления γL = 0,5, в двухдисковом сцеплении для среднего диска γL = 0,5, для нажимного γL = 0,25);
Δt – увеличение температуры диска при одном трогании автомобиля с места, которое не должно быть больше 15 о ;
С – удельная теплоемкость; для чугуна С = 482Дж/кг∙К [8].
Выступы и шипы, соединяющие нажимный диск с маховиком, рассчитывают на смятие. Условие работоспособности поверхности, подвергаемой смятию:
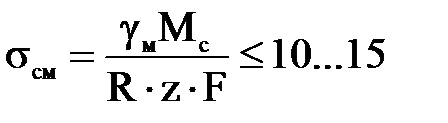
где γм – коэффициент, определяющий долю момента, передаваемого рассматриваемым диском (γм = γL);
R – расстояние от центра тяжести площади контакта сминаемых поверхностей до оси сцепления, м;
z – число выступов или шипов;
F – площадь контакта, м 2 .
Расчет рычагов выключения сцепления производится по допустимым напряжениям изгиба:
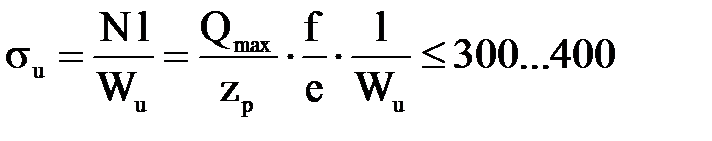
где l – расстояние от точки приложения силы N до опасного сечения (рисунок 6.1);
Wu – момент сопротивления изгибу опасного сечения, м 3 ;
Qmax – суммарная сила упругости нажимных пружин при выключенном сцеплении, кН;
f и е – плечи рычага, м;
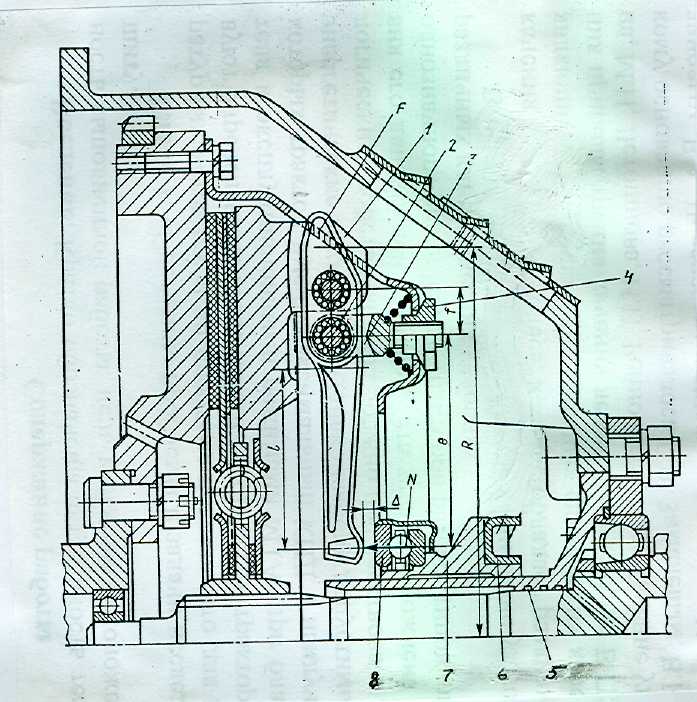
Рисунок 6.1 Расчетные размеры нажимного диска и рычага выключения:
1 – проушина; 2 – ось; 3 – опорная вилка; 4 – регулировочная гайка; 5 – передняя крышка коробки передач; 6 – вилка выключения; 7 – муфта выключения сцепления; 8 – упорный шарикоподшипник.
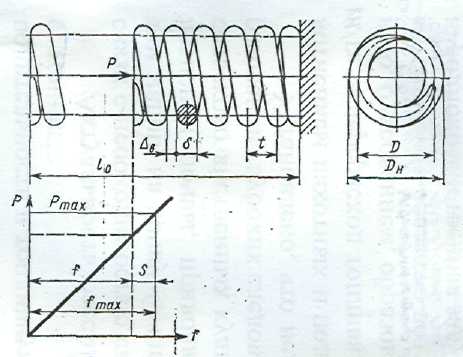
Расчет пружины выполняют для определения ее размеров, обеспечивающих необходимую характеристику пружины (рисунок 6.2). Нажимное усилие Р, создаваемое одной пружиной, является следствием ее деформации на величину f при установке на место. При выключении сцепления деформация пружины увеличивается на величину хода s нажимного диска, в результате чего сила упругости возрастает до значения Рmax, которое и является расчетной нагрузкой на пружину.
Обычно принимают Рmax =1,2 Р и из условия прочности пружины находят диаметр проволоки δ, а затем средний диаметр D витка по формулам
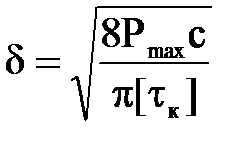
где с – индекс пружины; с = D/δ = 6÷9; [τк] – допускаемое напряжение при кручении проволоки; [τк] = 500÷700 МПа [9].
Число рабочих витков ip пружины и ее максимальная деформация fmax связаны зависимостью
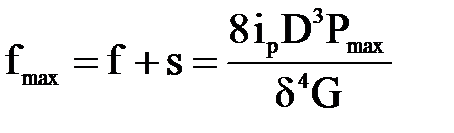
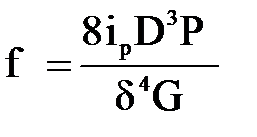
Рисунок 6.2. Нажимная пружина и ее характеристика
Решив полученное выражение относительно iр, имеем

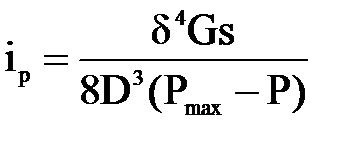
где G – модуль упругости второго рода; для стальной проволоки (сталь 65 или 65Г) G = (8,0 ÷8,3) 10 4 МПа [8].
Длина пружины в свободном состоянии
где iо – полное число витков; io = ip + 2; Δв – зазор между витками при выключенном сцеплении; принимают Δв = (0,5 ÷ 1,5) 10 -3 м.
Расчет привода сцепления.
Расчет привода производят для определения его передаточного числа и усилия на педали iп которые должны обеспечивать удобство и легкость управления. В выполненных конструкциях i = 24…45. Согласно схемам (рисунок 6.3) передаточные числа механического и гидравлического приводов соответственно равны:
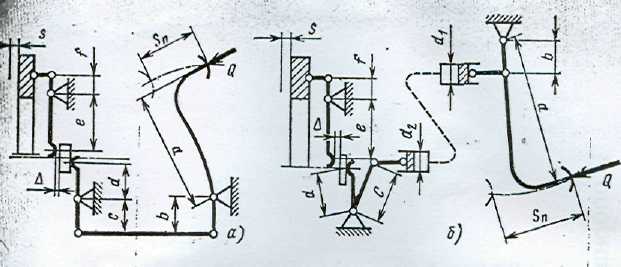
Рисунок. 6.3 Схема привода механизма выключения сцепления:
а — механического; б – гидравлического.
Для удобства управления сцеплением необходимо, чтобы при проектировании механического привода были удовлетворены условия гидравлического привода:
Источник статьи: http://studopedia.ru/6_67775_osnovi-rascheta-tipovih-elementov-friktsionnih-stsepleniy.html
Порядок расчета сцепления
1. Выбираем, коэффициент запаса сцепления 
Таблица 1.1 – Зависимость коэффициента запаса сцепления 
| Автомобиль | Условия работы | Коэффициент запаса сцепления  |
| Легковой автомобиль | Норма | 1,4÷1,7 |
| Грузовой автомобиль | Норма | 1,6÷2 |
| Тяжелые условия | 2÷2,5 |
Принимаем коэффициент запаса сцепления для автопогрузчика 
2. Определяем необходимый момент трения сцепления

Определяем однодисковое или двухдисковое сцепление будем рассчитывать. Критерием выбора сцепления является передаваемый крутящий момент. Однодисковое сцепление, применяют, если передаваемый крутящий момент не превышает 800 Нм, при передаче крутящего момента большей величины используют двухдисковое сцепление.
По расчетам момент трения сцепления составляет 378 Нм, следовательно, рассчитываем однодисковое сцепление, т.е. число пар поверхностей трения 
3. Определяем средний радиус фрикционной накладки, для этого выбираем наружный и внутренний диаметры фрикционного диска (рис. 1.1). Наружный диаметр фрикционной накладки определяем по эмпирической формуле

где А – коэффициент режима включения сцепления, (таблица 1.2). Принимаем коэффициент режима включения сцепления А = 3,6.
Таблица 1.2 – Зависимость коэффициента режима включения сцепления от типа автомобиля и условий работы
| Автомобиль | Условия работы | Коэффициент режима включения сцепленияА |
| Легковой автомобиль | Норма | 4,7 |
| Грузовой автомобиль | Норма | 3,6 |
| Тяжелые условия | 1,9 |


Рис.1.1. Размеры фрикционной накладки диска сцепления
Внутренний диаметр фрикционного диска сцепления ориентировочно выбирается из условия

Ориентируясь на ассортимент выпускаемой промышленностью фрикционных накладок, выбираем из следующего размерного ряда, 
Из данного ряда выбираем фрикционный диск сцепления 254/150, и определяем средний радиус (рис. 1.1)

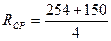
4. Определяем площадь поверхности трения диска сцепления с учетом площади необходимой для крепления фрикционной накладки с помощью заклепок

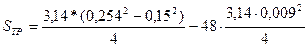
5. Определяем давление на фрикционные накладки,

где µ — коэффициент трения накладок.
Коэффициент трения фрикционной накладки о чугун находится в диапазоне от 0,25 до 0,4. Принимаем µ = 0,3.
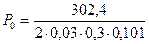
6. Определяем суммарное нажимное усилие создаваемое нажимными пружинами


Тогда усилие создаваемое нажимной пружиной

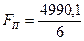
7. Определяем диаметр проволоки пружины

где 







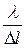
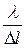



8. Определяем число рабочих витков пружины

где 


9. Определяем предварительное сжатие пружины


10. Максимальное усилие сжатия пружины

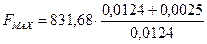
11. Определяем наибольшие напряжения в пружине при выключении сцепления
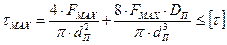


Рис. 1.2. Схема нажимной пружины:
а) пружина в свободном состоянии;
б) максимально сжатая пружина
Рис. 1.3. Схема фрикционного сцепления:
а) включенное сцепление; б) выключенное сцепление
1 – маховик; 2 – ведомый диск сцепления; 3 – кожух сцепления; 4 – нажимной диск; 5 – нажимные пружины (количество от 6 до 24); 6 — выжимной подшипник; 7 – вилка выключения сцепления; 8 – рычаг нажимного диска; 9 – первичный вал.
12. Свободная длина пружины (рис. 1.2)

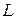
Задача
Определить, как изменится коэффициент запаса сцепления 

1. Определяем предварительное сжатие пружины с учетом износа ведомого диска сцепления


2. Определяем усилие создаваемое нажимной пружиной с учетом износа ведомого диска сцепления


3. Определяем суммарное нажимное усилие создаваемое нажимными пружинами с учетом износа ведомого диска сцепления


4. Определяем момент трения сцепления с учетом износа ведомого диска сцепления
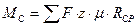

5. Определяем коэффициент запаса сцепления 


Коэффициент запаса сцепления 
Источник статьи: http://poisk-ru.ru/s66873t1.html