Сила тяги автомобиля движущегося по наклонной плоскости

Движение по наклонной плоскости тела: скорость, трение, время

Динамика и кинематика — это два важных раздела физики, которые изучают законы перемещения объектов в пространстве. Первый рассматривает действующие на тело силы, второй же занимается непосредственно характеристиками динамического процесса, не вникая в причины того, что его вызвало. Знание этих разделов физики необходимо применять для успешного решения задач на движение по наклонной плоскости. Рассмотрим этот вопрос в статье.

Основная формула динамики

Конечно же, речь идет о втором законе, который постулировал Исаак Ньютон в XVII веке, изучая механическое движение твердых тел. Запишем его в математической форме:

Действие внешней силы F¯ вызывает появление линейного ускорения a¯ у тела с массой m. Обе векторные величины (F¯ и a¯) направлены в одну и ту же сторону. Сила в формуле является результатом действия на тело всех сил, которые присутствуют в системе.

В случае движения вращения второй закон Ньютона записывается в виде:

Здесь M и I — моменты силы и инерции, соответственно, α — угловое ускорение.

Формулы кинематики

Решение задач на движение по наклонной плоскости требует знания не только главной формулы динамики, но и соответствующих выражений кинематики. Они связывают в равенства ускорение, скорость и пройденный путь. Для равноускоренного (равнозамедленного) прямолинейного движения применяются следующие формулы:

Здесь v₀ — значение начальной скорости тела, S — пройденный за время t путь вдоль прямолинейной траектории. Знак «+» следует поставить, если скорость тела увеличивается с течением времени. В противном случае (равнозамедленное движение) следует использовать в формулах знак «-«. Это важный момент.

Если движение осуществляется по круговой траектории (вращение вокруг оси), тогда следует использовать такие формулы:

Здесь α и ω — угловые ускорение и скорость, соответственно, θ — угол поворота вращающегося тела за время t.

Линейные и угловые характеристики друг с другом связаны формулами:

Здесь r — радиус вращения.

Движение по наклонной плоскости: силы

Под этим движением понимают перемещение некоторого объекта вдоль плоской поверхности, которая наклонена под определенным углом к горизонту. Примерами может служить соскальзывание бруска по доске или качение цилиндра по металлическому наклоненному листу.

Для определения характеристик рассматриваемого типа движения необходимо в первую очередь найти все силы, которые действуют на тело (брусок, цилиндр). Они могут быть разными. В общем случае это могут быть следующие силы:

• тяжести;
• реакции опоры;
• трения качения и/или скольжения;
• натяжение нити;
• сила внешней тяги.

Первые три из них присутствуют всегда. Существование последних двух зависит от конкретной системы физических тел.

Чтобы решать задачи на перемещение по плоскости наклонной необходимо знать не только модули сил, но и их направления действия. В случае, если тело по плоскости скатывается, сила трения неизвестна. Однако она определяется из соответствующей системы уравнений движения.

Методика решения

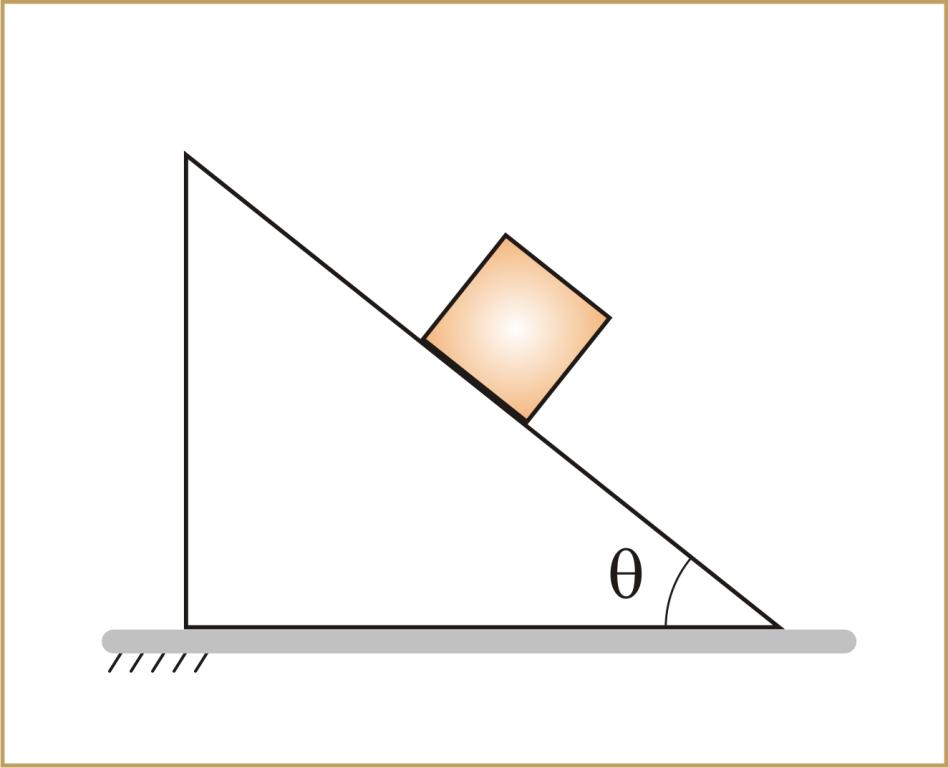
Решения задач данного типа начинается с определения сил и их направлений действия. Для этого в первую очередь рассматривают силу тяжести. Ее следует разложить на два составляющих вектора. Один из них должен быть направлен вдоль поверхности наклонной плоскости, а второй должен быть ей перпендикулярен. Первая составляющая силы тяжести, в случае движения тела вниз, обеспечивает его линейное ускорение. Это происходит в любом случае. Вторая равна силе реакции опоры. Все эти показатели могут иметь различные параметры.

Сила трения при движении по наклонной плоскости всегда направлена против перемещения тела. Если речь идет о скольжении, то вычисления довольно просты. Для этого следует использовать формулу:

Где N — реакция опоры, µ — коэффициент трения, не имеющий размерности.

Если в системе присутствуют только указанные три силы, тогда их результирующая вдоль наклонной плоскости будет равна:

Здесь φ — это угол наклона плоскости к горизонту.

Зная силу F, можно по закону Ньютона определить линейное ускорение a. Последнее, в свою очередь, используется для определения скорости движения по наклонной плоскости через известный промежуток времени и пройденного телом расстояния. Если вникнуть, то можно понять, что все не так уж и сложно.

В случае, когда тело скатывается по наклонной плоскости без проскальзывания, суммарная сила F будет равна:

Где F_r — сила трения качения. Она неизвестна. Когда тело катится, то сила тяжести не создает момента, поскольку приложена к оси вращения. В свою очередь, F_r создает следующий момент:

Учитывая, что мы имеем два уравнения и две неизвестных (α и a связаны друг с другом), можно легко решить эту систему, а значит, и задачу.

Теперь рассмотрим, как использовать описанную методику при решении конкретных задач.

Задача на движение бруска по наклонной плоскости

Деревянный брусок находится в верхней части наклонной плоскости. Известно, что она имеет длину 1 метр и располагается под углом 45 o . Необходимо вычислить, за какое время брусок опустится по этой плоскости в результате скольжения. Коэффициент трения принять равным 0,4.

Записываем закон Ньютона для данной физической системы и вычисляем значение линейного ускорения:

a = g*(sin(φ) — µ*cos(φ)) ≈ 4,162 м/с 2

Поскольку нам известно расстояние, которое должен пройти брусок, то можно записать следующую формулу для пути при равноускоренном движении без начальной скорости:

Откуда следует выразить время, и подставить известные значения:

Таким образом, время движения по наклонной плоскости бруска составит меньше секунды. Заметим, что полученный результат от массы тела не зависит.

Задача со скатывающимся по плоскости цилиндром

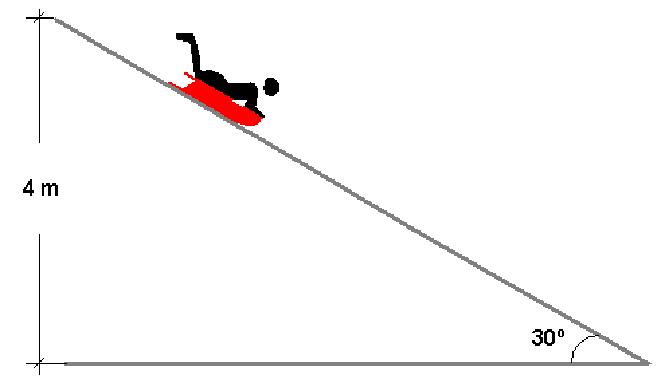
Цилиндр радиусом 20 см и массой 1 кг помещен на наклонную под углом 30 o плоскость. Следует вычислить его максимальную линейную скорость, которую он наберет при скатывании с плоскости, если ее длина составляет 1,5 метра.

Запишем соответствующие уравнения:

Момент инерции I цилиндра вычисляется по формуле:

Подставим это значение во вторую формулу, выразим из нее силу трения F_r и заменим полученным выражением ее в первом уравнении, имеем:

m*g*sin(φ) — 1/2*m*a = m*a =>

Мы получили, что линейное ускорение не зависит от радиуса и массы скатывающегося с плоскости тела.

Зная, что длина плоскости составляет 1,5 метра, найдем время движения тела:

Тогда максимальная скорость движения по наклонной плоскости цилиндра будет равна:

Подставляем все известные из условия задачи величины в конечную формулу, получаем ответ: v ≈ 3,132 м/c.

Источник статьи: http://fb.ru/article/443466/dvijenie-po-naklonnoy-ploskosti-tela-skorost-trenie-vremya

Сила тяги автомобиля движущегося по наклонной плоскости

Введение

Нашу современную жизнь трудно представить без автомобиля. Нет такой профессии на Земле, представитель которой не нуждался бы в автомобиле. На автомобиле или на автобусе мы добираемся до места назначения. Когда выходишь из дома, то почти сразу мы видим автомобиль.

Первый автотранспорт был изобретен много лет назад. Он восхищал своей эксклюзивностью и новаторством. Сейчас в мире представлены тысячи различных моделей машин, которые рассчитаны на разных потребителей. Но часто ли водители задумываются над следующими вопросами.

Каковы причины движения автомобиля? Какие силы действуют на автомобиль?

В нашей работе мы попытаемся ответить на это вопросы, используя специальную литературу. Рассмотрим какие внешние силы действуют на автомобиль во время движения по прямой и наклонной поверхности. Определим какие силы препятствуют, а какие способствуют движению автомобиля. Отдельное внимание уделим процессу торможения, так как с помощью тормозов можно не только остановить и удержать машину на месте, но и преодолеть скользкий участок, опасный поворот, развернуться и даже перескочить неширокую канаву или выбоину.

Силы, действующие на автомобиль

Автомобиль, преодолевающий подъем, одновременно движется вверх и вперед. В общем случае на подъеме при ускоренном перемещении автомобиля на него действуют силы, движущие его, силы оказывающие сопротивление движению автомобиля, и силы, составляющие нормальные реакции дороги на передние Z_п и задние Z_з колеса, вызванные перпендикулярной плоскости дороги составляющей силы тяжести автомобиля.

Покрышка соприкасается с дорогой бесконечно большим числом точек. В каждой из этих точек на покрышку действует бесконечно малая сила — элементарная реакция дороги. Равнодействующую элементарных сил, которая действует со стороны дороги на колесо в области контакта, называют реакцией дороги.

Силы, движущие автомобиль, возникают в результате взаимодействия ведущих колес автомобиля с дорогой и называются силами тяги F_т (рис. 1).

К силам, оказывающим сопротивление движению автомобиля, относятся силы сопротивления качению передних Р_ск.п. и задних Р_ск.з. колес, действующие в плоскости дороги; сила сопротивления подъему Р_сп, сила сопротивления воздуха F_св, сила инерции F_и , приложенная к центру масс ЦМ автомобиля и на­зываемая силой сопротивления разгону.

Силы Z_п и Z_з составляют нормальные реакции дороги на передние и задние колеса соответственно. Они вызваны перпендикулярной плоскости дороги, составляющей GN силы тяжести G автомобиля с полной нагрузкой.

Рис.1. Внешние силы, действующие на автомобиль во время движения: ЦМ- центр масс; G — Сила тяжести автомобиля с полной нагрузкой;

GN — составляющая силы тяжести, перпендикулярная плоскости дороги; Р_сп _ сила сопротивления подъему; Р_ск.п , Р_ск.з — сила сопро­тивления качению передних и задних колес; F_св — сила сопротивления воздуха; F_т — сила тяги; F_и — сила инерции; a — угол, характеризующий крутизну подъема; Н- превышение дороги; S- заложение дороги; Zn, Z_з— нормальные реакции дороги на передние и задние колеса.

Сила сопротивления качению

Сила сопротивления качениюР_ск постоянно мешает движению и представляет собой целую совокупность сил. Это силы, деформирующие и перемещающие грунт; деформирующие шины; силы трения колес о колею; силы, образующиеся при преодолении выбоин, и т. п.

Принято считать, что:

где: Р_ск — сила сопротивления качению;

f = 0,015 — 0,3 — коэффициент сопротивления качению, учитывающий состояние дороги, давление в шинах и пр.;

G — сила тяжести автомобиля.

Сила сопротивления качению Р_ск составляет подобающую долю от силы тяжести автомобиля.

Сила сопротивления подъему

Сила сопротивления подъемуР_сп — Крутизну подъема охарактеризовывают углом в градусах (см. рис. 1) или же уклоном дороги i, который представляет собой отношение превышения Н дороги к заложению S, т. е. Силу тяжести G автомобиля, преодолевающего подъем, можно разложить на две составляющие: на силу Р_сп, параллельную дороге, и силу Gn=G-cosα, перпендикулярную ей.

Силу Р_сп= G-sinα, называют силой сопротивления подъему, где

Также силу сопротивления подъему выражают формулой

При перемещении на спуске сила Р_сп ориентирована в сторону перемещения автомобиля и, следовательно, меняет свой знак (рис. 1, в) и, в отличие от силы сопротивления качению, может стать и движущей. Вследствие этого угол а и уклон дороги i считают положительными при перемещении автомобиля на подъеме и отрицательными при его перемещении на спуске.

При перемещении автомобиля на подъеме силу Р_сп можно объединить с Р_ск, а поскольку обе эти силы пропорциональны силе тяжести автомобиля, то:

При перемещении автомобиля под уклон

Сила сопротивления воздуха (аэродинамическое сопротивление)

Сила сопротивления воздуха F_св— данная сила считается следствием давления встречных частиц воздуха на движущийся автомобиль, разрежения, образующегося позади автомобиля, завихрения воздуха вокруг автомобиля и трения воздуха о поверхность автомобиля. В каждой точке поверхности автомобиля в итоге соприкосновения его с воздушной средой появляются элементарные силы, нормальные к поверхности и касательные к ней. Для упрощения расчетов элементарные силы сопротивления воздуха, распределенные по всей поверхности автомобиля, заменяют сосредоточенной силой сопротивления воздуха F_CB. Опытным путем установлено, что сила сопротив­ления воздуха равна

k_в — коэффициент сопротивления воздуха, зависящий от формы и качества отделки поверхности автомобиля 0,20 — 0,30H·m 4 ;

S_л — лобовая площадь автомобиля;

V — скорость движе­ния автомобиля.

Из формулы видно, что сопротивление воздуха находится в зависимости от скорости автомобиля, его обтекаемости, величины площади попе­речного сечения, плотности воздуха. Существенное значение F_св приобретает только при высоких скоростях, так как зависит от квадрата скорости.

Сила, разгоняющая автомобиль.

Для автомобиля характерным считается неравномерное движение. Показателями разгона являются ускорение, время и путь разгона. В общем случае перемещения автомобиля сила тяги F_т уравновешивается силами сопротивления перемещения:

При разгоне автомобиля, т. е. при перемещении автомобиля с ускорением а, появляется сила инерции F_и автомобиля, противодействующая разгону, равная

где m — масса автомобиля;

а — ускорение автомобиля.

Влияние инерционного момента вращающихся масс учитывается коэффициентом  относительного увеличения массы автомобиля, предусматривающим воздействие вращающихся масс, показывающим, во сколько раз сила, необходимая для ускорения автомобиля, больше силы инерции его поступательно движущейся массы.

В соответствии с этим общая сила сопротивления разгону

n_кп — передаточное число коробки передач, на которой производится разгон.

Мощность, которая имеется для обеспечения ускорения, представляет собой разность между мощностью, требующейся при данных условиях для преодоления сопротивления движения, и мощностью, подводимой к ведущим колесам.

Мощность, важная для перемещения автомобиля с ускорением

V — скорость автомобиля.

Из приведенной формулы видно, что чем автомобиль легче, тем большее ускорение получится развить при схожей мощности мотора.

В случае если автомобиль движется без разгона (Fp = 0 и F_и = 0), вся сила тяги тратится на преодоление сил сопротивления, и равна:

В случае, когда автомобиль замедляет ход, сила тяги становится меньше суммарной величины сил, препятствующих перемещению.

Сила тяги автомобиля.

Энергия от мотора к ведущим колесам передается через трансмиссию: сцепление, коробку передач, карданную передачу, главную передачу, дифференциал и полуоси. Благодаря наличию в трансмиссии коробки передач и главной передачи, суммарный крутящий момент М_кр на ведущих колесах автомобиля больше момента мотора М_дв.

Крутящий момент М_кр вызывает в месте контакта колеса с дорогой касательную реакцию дороги, движущую автомобиль, т. е. силу тяги. На теоретическом уровне ведущее колесо взаимодействует с дорогой в одной точке (практически же — в «пятне контакта»). Активной в этой точке является сила, с которой колесо «толкает» дорогу. Вот тут-то и появляется ответная (реактивная) сила F_T реакции дороги, которая «толкает» машину. Величина силы тяги равна отношению крутящего момента на полуосях к радиусу ведущих колес, т. е., М_кр -крутящий момент на колесе,

R — статический радиус колеса.

Таким образом, для определения силы тяги необходимо знать радиус R ведущего колеса и момент М_кр. Так как на колеса автомобиля установлены эластичные пневматические шины, то радиус колеса во время движения изменяется под влиянием действующих на колесо сил. Различают статический радиус колеса ( расстояние от поверхности дороги до оси неподвижного колеса, значение которого приводится в технической характеристике шины), динамический радиус колеса (расстояние от поверхности дороги до оси катящегося колеса) и радиус качения колеса (радиус условно недеформирующегося кольца, имеющего с данным эластичным колесом схожую угловую и линейную скорости). Для простоты расчетов силы тяги считают радиус колеса постоянным и равным статическому радиусу колеса.

Сила сцепления шины с дорогой

Сила сцепления покрышки с дорогой Р_сц. Для того чтобы автомобиль имел возможность стабильно ехать, тормозить и поворачивать, необходимо надежное сцепление покрышек с дорогой. Сила сцепления Р_сц находится в зависимости от сцепного веса автомобиля и скорости перемещения автомобиля, а также от состояния дороги и покрышек: где:

G_сц — сцепной вес автомобиля,

Коэффициент сцепления покрышек с дорогой определяет проходимость автомобиля при перемещении по влажному грунту и по скользкой дороге.

Сцепной вес автомобиля возможно, увеличить, увеличивая количество ведущих колес или смещая центр тяжести в сторону ведущего моста.

От сцепления колес с дорогой зависят максимально вероятные силы тяги и торможения, а также боковая устойчивость автомобиля.

Если сила тяги приложенная к колёсам превышает силу сцепления, то при попытке тронуться с места ведущие колеса автомобиля пробуксовывают. Если тормозная сила колеса больше силы сцепления, колесо блокируется. И в том и в ином случаях возникает юз — проскальзывание колеса относительно опоры. Юз наступает тогда, когда скорость точки касания колеса с дорогой не равна нулю относительно дороги. В случае если эта точка неподвижна относительно дороги, колесо не будет проскальзывать до тех пор, пока действующие на него в точке касания силы не превысят силы трения покоя.

Автомобиль движется благода­ря наличию силы трения покоя. Ведь, если бы этого трения не было, колеса всегда проскальзывали бы относительно опоры, т. е. прокручивались бы при попытке разогнать автомобиль и блокировались бы при попытке его остановить. И если на льду колесо буксует или скользит, это означает, что соответственно силы тяги или торможения превышают силу трения (Р_сц применительно к автомобилям). Очевидно, что условием движения автомобиля без юза являются соотношения:

F_T 2 /2) превращается в тепло. Максимально возможное при торможении замедление:

g — ускорение свободного падения.

Но это лишь теоретически возможное замедление. Реально же значение замедления а меньше по многим причинам.

Во время экстренного торможения тормозной путь окажется равен:

V — скорость автомобиля, измеряемая в м/с, в момент начала торможения;

а — максимально возможное замедление автомобиля при торможении.

Формулы наглядно демонстрируют, что, если в результате изменения дорожных или погодных условий значение ᵠ_сц упало, во столько же раз снижаются максимально возможные сила торможения и замедление автомобиля.

Длина тормозного пути прямопропорциональна квадрату скорости автомобиля в момент начала торможения.

Из практики известно, что юз задних колес наступает чаще юза передних так как при торможении у автомобиля опускается передняя часть.

Это объясняется тем, что при торможении автомобиля сила инерции F_H, которая приложена к ЦМ, действуя на плече Н (рис. 2, б), и тормозные силы Р_торм, лежащие в плоскости дороги, образуют относительно ЦМ тормозной момент М_торм, который вызывает перераспределение нормальных нагрузок между передним и задним мостами. При этом нагрузка на передние колеса увеличивается, а на задние уменьшается. Поэтому нормальные реакции Z_п и Z_з, действующие соответственно на передние и задние колеса автомобиля во время торможения, значительно отличаются от нагру­зок G_п и G_з, которые они воспри­нимают в статическом состоянии

Во время резкого торможения автомобиля реакция на переднюю ось у легковых автомобилей может возрасти в 1,5 — 2 раза, а на заднюю ось уменьшиться в 0,5 — 0,7 раза.

Степень распределения суммарной нагрузки по осям при торможении зависит от высоты расположения центра масс и от расстояния между осями. С уменьшением нагрузки на заднюю ось допустимые тормозные усилия на задних колесах уменьшаются, а на передних — увеличиваются; следовательно, при торможении задние колеса более склонны к юзу.

Рис.2. Силы, действующие на ав­томобиль при торможении и остановке: ЦМ — центр масс; Н — расстояние между ЦМ и пло­скостью дороги; Р_торм — тор­мозная сила; М_торм — тормозной момент; G — вес автомобиля;G_сц — сцепной вес автомобиля

Рис.3. Силы сцепления колеса с дорогой, действующие в пятне контакта колеса: F_т -сила тяги; F́_т— сила тяги при интенсивном разгоне; Р_торм -сила торможения;

Р́_торм — сила торможения при интенсивном замедлении; Р́_бок.сц. — поперечная сила сцепления при интенсивном разгоне или торможении; Р_бок.сц. — поперечная сила сцепления; Р_сц — сила сцепления.

В процессе торможения реакция на передние колеса увеличивается, а на задние уменьшается. Поэтому для полной реализации силы сцепления при экстренном торможении необходимо, чтобы тормозные силы были пропорциональны нормальным реакциям. Исходя из этого делают так, чтобы передние колеса тормозили настолько сильнее, насколько больше при торможении они прижимаются к дороге. Это позволяет при торможении получить наибольшую тормозную силу, поскольку сила сцепления каждого колеса пропорциональна приходящейся на него нагрузке.

Для того чтобы предотвратить блокировку задних колёс применяется регулирование давления в тормозном приводе, которое обеспечивает ограничение роста давления в тормозных механизмах задних колес при уменьшении реакции на задние колеса автомобиля. Клапан регулятора давления перекрывает подвод жидкости к тормозным механизмам задних колес в случае, когда давление в ее тормозном контуре возрастает до предельного, угрожающего блокировкой колес. Более совершенные антиблокировочные системы с электронными датчиками скорости вращения колес предотвращают блокировку колес при любых значениях коэффициента сцепления.

Заключение

В настоящей работе были рассмотрены силы, действующие на автомобиль. К ним относятся:

Сила сопротивления качению, которая всегда препятствует движению и возникает вследствие деформации шин и поверхности дороги;

Сила сопротивления подъему может быть направлена как в сторону движения, так и против него. В процессе подъема она действует в направлении, противоположном движению, и является силой сопротивления движению. При спуске эта сила, направленная в сторону движения, становится движущей;

Сила сопротивления воздуха зависит от коэффициента сопротивления воздуха, лобовой площади и скорости движения автомобиля;

Сила разгоняющая автомобиль, которая зависит от ускорения, времени и пути разгона;

Сила тяги автомобиля возникает при передачи крутящего момента с двигателя на колеса и для её определения необходимо знать радиус ведущего колеса;

Сила сцепления шины с дорогой зависит от сцепного веса автомобиля и скорости движения, она нужна для того, чтобы автомобиль мог устойчиво двигаться, тормозить и поворачивать.

Эти силы, действующие на автомобиль во время движения, влияют на изменения показателей эффективности работы автомобиля. К этим показателям можно отнести скоростные свойства автомобиля, топливная экономичность, износ деталей автомобиля, аэродинамические свойства.

Учет этих показателей позволит повысить эффективность использования автомобильного транспорта, и сократить число дорожно-транспортных происшествий.

Литература

Ваганов В.И. Вождение автотранспортных средств / Ваганов В.И., Рывкин А.А. — М.:Транспорт, 1990 – 224 с.

Горбачев М.Г. Безопасное вождение современного автомобиля / Горбачев М.Г. – м.: Рипол Классик, 2007 — 232

Калисский В.С. Автомобиль: Учебник водителя третьего класса / Калиссий В.С., Манзон А.И., Нагула Г.Е. – 5-е изд.,стереотип. – М.: Транспорт, 1980. – 368 с.

Николенко В.В. Вождение автомобиля. Практическое пособие / Николенко В.В. – 1991 — 62 с.

Тимовский А.А. Основы управления автомобилем и безопасность дорожного движения / Тимовский А.А., Нестеренко В.Б. – Арий, — 2009, 146 с.

Шухман Ю.И. Основы управления автомобилем и безопасность движения / Шухман Ю.И. – м,: ООО «Книжное издательство «За рулем», 2006.-160 с.

Источник статьи: http://school-science.ru/5/11/34481