Тормозная сила и уравнение движения автомобиля при торможении
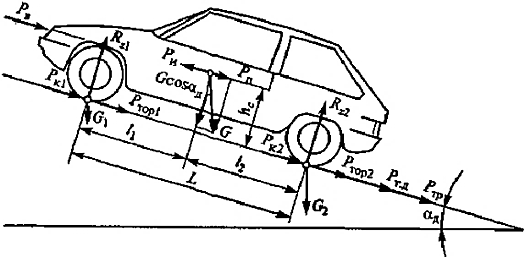
При торможении элементарные силы трения (рис.8.1), распределенные по поверхности фрикционных накладок, создают результирующий момент трения – тормозной момент Мтор, направленный в сторону, противоположную вращению колеса. Между колесом и дорогой возникает тормозная сила Ртор.
Максимальная тормозная сила равна силе сцепления шины с дорогой. Современные автомобили имеют тормозные механизмы на всех колесах.
Pт.д – сила трения в двигателе, приведенная к ведущим колесам;
Ртр – сила, затрачиваемая на привод агрегатов трансмиссии и дополнительное оборудование при торможении
Рисунок 8.1– Силы, действующие на автомобиль при торможении
У двухосного автомобиля максимальная тормозная сила:
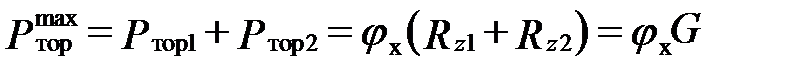 | (8.1) |
где Ртор1, Ртор2 – тормозная сила между дорогой и шинами колес соответственно передней и задней осей;
Rz1, Rz2 – нормальные реакции, соответственно, на колесах передней и задней осей (значения численно равны весу, приходящегося, соответственно, на переднюю и заднюю оси);
φx – коэффициент сцепления шин с дорогой.
Следует отметить, что предельное значение тормозной силы определяется коэффициентом сцепления шин с дорогой.
Уравнение движения автомобиля при его торможении на подъеме можно получить из уравнения силового баланса, спроецировав все силы, действующие на автомобиль, на плоскость дороги:
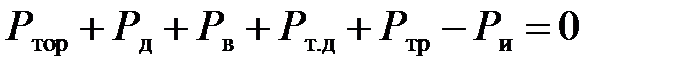 | (8.2) |
При торможении с выключенным сцеплением (на нейтральной передаче) и учитывая, что скорость автомобиля во время торможения падает, то уравнение (8.2) запишется в следующем виде:
После преобразования, с учетом ранее изложенного материала уравнение торможения автомобиля на негоризонтальном участке дороги примет вид:
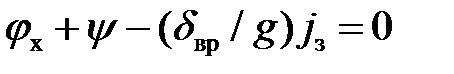 | (8.3) |
где δв – коэффициент учета вращающихся масс;
jз – замедление автомобиля.
Замедление автомобиля при торможении определяется уравнением силового баланса:
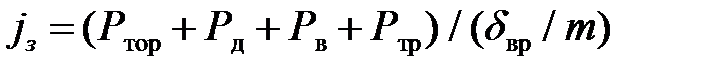 | (8.4) |
где m – масса автомобиля, кг.
Если тормозные силы на всех колесах достигли значения сил сцепления, то, пренебрегая силами Рв и Ртр получим: 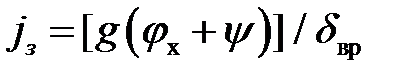
Коэффициент φх обычно значительно больше коэффициента ψ, поэтому при торможении автомобиля на грани блокировки колес величиной ψ можно пренебречь, а при торможении с отключенным двигателем можно принять δвр≈1.
Для горизонтального участка дороги уравнение торможения автомобиля будет иметь вид: 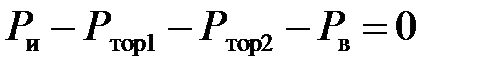
Замедление при торможении определим из выше приведенного уравнения, представив Ри в развернутом виде:
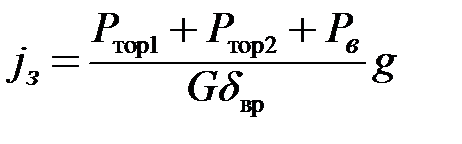 | (8.5) |
Дата добавления: 2016-02-27 ; просмотров: 5386 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ
Источник статьи: http://helpiks.org/7-20714.html
Уравнения движения автомобиля при торможении



Пользуясь рис.2.1, можно записать
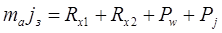
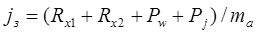
где, Rx1 и Rx2 – продольные реакции опорной поверхности, прикладываемые к передним и задним колесам;
Рw – сила лобового аэродинамического сопротивления;
Торможение, целью которого является максимально быстрая остановка, называется экстренным. Торможение, совершаемое с целью предотвратить ДТП, называется аварийным. На дорогах с высоким коэффициентом сцепления jз = 8…9 м/с 2 .
Плавное торможение jз = 2,5…3 м/с 2 называют служебным. Если конечная скорость при торможении равна нулю, его называют полным, если не равна – частичным.
При экстренном торможении продольные реакции могут достигать значений Rхмакс. Такой случай будем называть торможением с полным использованием сил сцепления.

|
При таких допущениях процесс торможения может быть описан графиком зависимости jз = f(t) (рис.2.2), называемым тормозной диаграммой. Начало координат соответствует моменту нажатия на тормозную педаль (начало торможения). На диаграмму для лучшей иллюстративности иногда наносят зависимость V = f(t). При возникновении аварийной ситуации водитель, приняв в результате оценки обстановки решение тормозить, переносит ногу с педали управления подачей топлива на тормозную педаль. Время tрв от момента, когда замечена опасность, до начала торможения называют временем реакции водителя. В зависимости от индивидуальных качеств, квалификации водителя, степени его утомленности, дорожной обстановки и т.п. tрв может изменяться в пределах 0,2…1,5 с. При расчетах принимают среднее значение tрв = 0,8 с.
После начала торможения время tс, называемое временем запаздывания, затрачивается на перемещение элементов тормозного привода на величину зазоров, имеющихся между ними в нерабочем положении, нарастание давления жидкости или воздуха в трубопроводах и рабочих аппаратах гидравлического или пневматического привода до значения, необходимого для преодоления усилий возвратных пружин колодок и перемещения колодок до соприкосновения их фрикционных накладок с тормозными дисками или барабанами. Время tс зависит от типа тормозного привода и тормозных механизмов, а также технического состояния тормозной системы. У технически исправной тормозной системы с гидроприводом и дисковыми тормозными механизмами tс = 0,05…0,07 с, с барабанными тормозными механизмами tс = 0,15…0,20 с, у систем с пневмоприводом tс = 0,2…0,4 с. Время tс возрастает при увеличении зазоров в тормозных механизмах, попадании воздуха в гидропривод, падении давления в ресивере пневмопривода и др.
С момента соприкосновения фрикционных элементов тормозных механизмов реакция Rх, а в результате этого и замедление увеличиваются от 0 до значения, соответствующего установившемуся значению сил, приводящих в действие тормозные механизмы. Время tн, затрачиваемое на этот процесс, называют временем нарастания замедления jз.н. В зависимости от типа автомобиля, состояния дороги, дорожной ситуации, квалификации и состояния водителя, состояния тормозной системы tн может изменяться в пределах 0,05 … 2 с. Оно возрастает с увеличением Gа и jх (поскольку увеличиваются разжимные силы в тормозных механизмах, необходимых для создания Rхмакс).
При наличии неисправной тормозной системы (наличие воздуха в гидроприводе, низкое давление воздуха в ресивере пневмопривода, попадание масла и воды на рабочие поверхности фрикционных элементов) значения tн существенно увеличиваются.
В расчетах можно принимать следующие значения tн: 0,05…0,2 с – для легковых автомобилей; 0,05…0,4 с – для грузовых автомобилей с гидроприводом; 0,15…1,5 с – для грузовых автомобилей с пневмоприводом; 0,2…1,3 с – для автобусов.
Переменное значение jз на участке tуст условно заменяют средним и считают установившимся, взяв за начало отсчета (t = 0) момент прекращения увеличения усилия на педаль.
Поэтому tуст называют временем установившегося замедления.
Время tр от начала отпускания тормозной педали до возникновения зазоров между фрикционными элементами называют временем растормаживания.
Время для разных тормозных систем
| Время запаздывания, tс, с | Время нарастания tн, с | ||||
| с гидро-приводом и дисковыми тормозными механизмами | с барабанными тормозными механизмами | с пневмо-приводом | для легковых а/м | для грузовых а/м с гидропри-водом | для грузовых а/м с пневмо-приводом |
| 0,05…0,07 | 0,15…0,20 | 0,2…0,4 | 0,05…0,2 | 0,05…0,4 | 0,15…1,5 |
Путь Sтс получают по формуле:
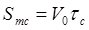
где Sтс — путь за время запаздывания, м;
V0 — начальная скорость торможения, км/ч;
tс — время запаздывания, с.
Путь Sтн получают по формуле:
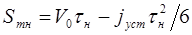
где Sтн — путь за время нарастания торможения, м;
tн — время нарастания торможения, с;
jуст — установившееся ускорение, м/с 2 .
Скорость V0уст, соответствующую началу движения с jуст найдем по формуле:
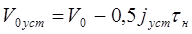
где V0уст — скорость при установившемся ускорении, м/ч.
Путь Sт.уст получают по формуле:
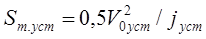
где Sт.уст — путь за время установившегося ускорения, м.
Зависимость V = f(t) на тормозной диаграмме описывается следующими отрезками: на участке tс прямой, параллельной оси абсцисс, на участке tн – квадратичной параболой, на участкеtуст – прямой с угловым коэффициентом равным jуст, поскольку 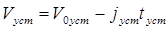
Источник статьи: http://studopedia.ru/16_115183_uravneniya-dvizheniya-avtomobilya-pri-tormozhenii.html
Задачи «разгон» и «торможение»
При кажущемся изобилии задач на прямолинейное равноускоренное движение все они могут быть сведены к задачам двух типов. Для этого необходимо выбрать ось X таким образом, чтобы ее положительное направление совпадало с направлением движения тела. В этом случае все задачи сводятся либо к задаче «разгон» (если a > 0), либо к задаче «торможение» (если a
Задача «Разгон»
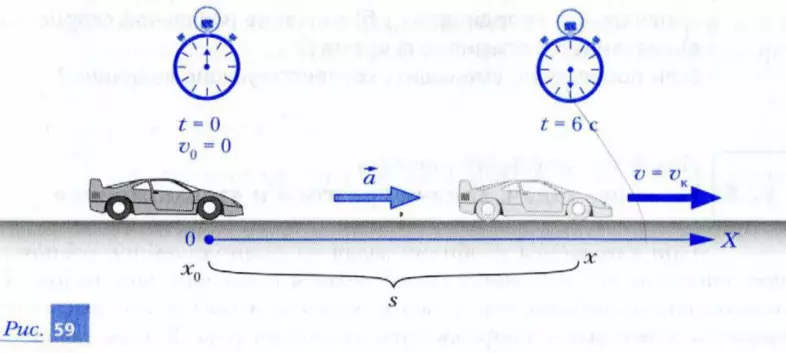
Гоночный автомобиль трогается с места, набирая скорость 30 м/с (108 км/ч) за время t = 6 с. Определите пройденный автомобилем за это время путь, считая движение автомобиля равноускоренным.
Решение.
Используем известную нам схему решения кинематических задач.
Шаг 1. Свяжем координатную ось X с дорогой, по которой разгоняется автомобиль. Начало отсчета поместим в то место, откуда автомобиль начинает разгон. Ось X направим по ходу движения автомобиля, как показано на рис. 59. В качестве единицы выберем 1 м. Включим часы (секундомер) в момент начала разгона.
Шаг 2. Определим в выбранной нами системе отсчета начальную координату автомобиля – x0 = 0.
Шаг 3. По условию начальная скорость автомобиля v0 = 0. Так как направление ускорения совпадает с положительным направлением оси X, то значение ускорения a будет положительным.
Шаг 4. Запишем зависимость координаты от времени при прямолинейном равноускоренном движении автомобиля с учетом данных задачи:
x = x0 + v0 · t + (a · t 2 ) / 2 = 0 + 0 + (a · t 2 ) / 2 = (a · t 2 ) / 2.
Шаг 4* (новый). Запишем зависимость значения скорости автомобиля от времени:
v = v0 + a · t = 0 + a · t = a · t.
Из этого выражения видно, что при положительном значении ускорения скорость автомобиля увеличивается со временем. При этом за каждую секунду значение скорости возрастает на величину, равную a · 1 (м/с).
Шаг 5. Условие окончания разгона до скорости vк имеет вид:
Шаг 6. Объединим составленные уравнения, присвоив каждому номер и название:
x = (a · t 2 ) / 2, (1) (закон движения автомобиля)
v = a · t, (2) (зависимость скорости от времени)
v = vк. (3) (условие окончания разгона)
Шаг 7. Решение уравнений. Чтобы ответить на вопрос задачи, необходимо решить уравнение (1), подставив в него время разгона 6 с и значение ускорения a. Однако значение ускорения нам пока не известно. Зато нам известны значения начальной и конечной скоростей автомобиля. Следовательно, мы можем найти значение ускорения. Для этого в условие окончания разгона (3) подставим из уравнения (2) значение скорости a · t в момент t = 6 с:
Подставив полученное значение a в уравнение (1), находим:
x = (a · t 2 ) / 2 = (5 · 6 2 ) / 2 = 90 (м).
Ясно, что s = x — x0 = 90 — 0 = 90 (м).
Как вы заметили, в отличие от задач о равномерном движении, в шаге 4 появилось дополнение, связанное с тем, что скорость равноускоренно движущегося тела изменяется со временем. В результате появилось новое уравнение – зависимость значения скорости от времени.
Задача «Торможение»
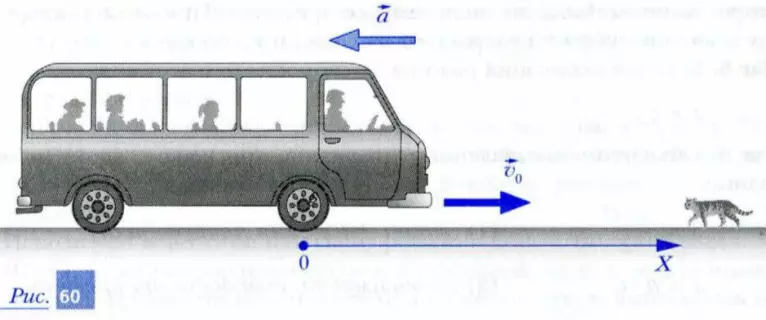
Автобус движется со скоростью, модуль которой равен 20 м/с (72 км/ч). Водитель автобуса замечает на дороге кошку и нажимает на педаль тормоза. Определите длину тормозного пути автобуса, если модуль ускорения при торможении |a| = 4 м/с 2 .
Решение.
Шаг 1. Систему отсчета выберем так, как показано на рис. 60.
Шаг 2. Начальная координата автобуса x0 = 0.
Шаг 3. Значение начальной скорости автобуса v0 = 20 м/с.
Шаг 4. С учетом шагов 1, 2 и 3 зависимость координаты автобуса от времени будет иметь вид:
x = x0 + v0 · t + (a · t 2 ) / 2 = 0 + 20 · t — (4 · t 2 ) / 2.
Внимание! Значение скорости автобуса уменьшается. Значит, направление вектора ускорения автобуса противоположно положительному направлению оси X. Поэтому мы подставили в формулу отрицательное значение ускорения (a = -4 м/с 2 ). При этом направление вектора начальной скорости совпадает с положительным направлением оси X. Поэтому значение скорости v0 положительно. Такие же знаки у величин v0 и a будут и в шаге 4*.
Шаг 4* (новый). Зависимость значения скорости от времени имеет вид:
v = v0 + a · t = 20 — 4 · t.
Видно, что при отрицательном значении ускорения a = -4 м/с 2 скорость автобуса со временем уменьшается. При этом за каждую секунду значение скорости изменяется на величину -4 м/с, т. е. уменьшается на 4 м/с.
Шаг 5. Запишем условие окончания торможения: v = 0, так как в искомый момент времени t автобус должен остановиться.
Шаг 6. Объединим составленные уравнения, присвоив каждому номер и название:
x = 0 + 20 · t — (4 · t 2 ) / 2, (1) (закон движения автобуса)
v = v0 + a · t = 20 — 4 · t, (2) (зависимость скорости от времени)
v = 0. (3) (условие окончания торможения)
Шаг 7. Решение уравнений. Чтобы найти тормозной путь, необходимо подставить в уравнение (1) время торможения автобуса. Эта величина нам неизвестна, но ее можно найти из уравнений (2) и (3). Для этого необходимо подставить в зависимость скорости от времени значение скорости в момент окончания торможения v = 0, после чего решить полученное уравнение:
20 — 4 · t = 0, t = 5 c.
Таким образом, автобус остановится через время t = 5 с.
Подставим найденное время торможения t = 5 с в уравнение (1) и найдем тормозной путь:
x = 20 · 5 — (4 · 5 2 ) / 2 = 50 (м).
Таким образом, длина тормозного пути автобуса равна 50 м.
Итоги
Если положительное направление оси X выбрать совпадающим с направлением движения тела, то все задачи на равноускоренное движение можно свести к двум типам:
1) задача «разгон» (a > 0, скорость тела увеличивается с течением времени);
2) задача «торможение» (a Если тело меняет направление своего движения, то рассматриваемый промежуток времени нужно разделить на интервалы, в течение каждого из которых тело движется только в одном направлении. При этом задача разделяется на несколько задач.
Упражнения
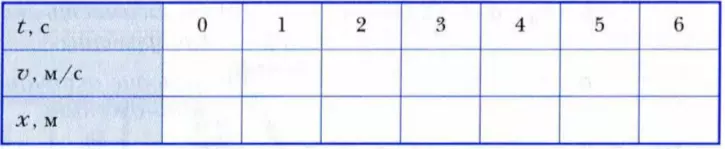
1. Заполните таблицу для разгоняющегося автомобиля, используя условия задачи 1 («разгон»). Как изменяются со временем: значение скорости; координата разгоняющегося автомобиля?
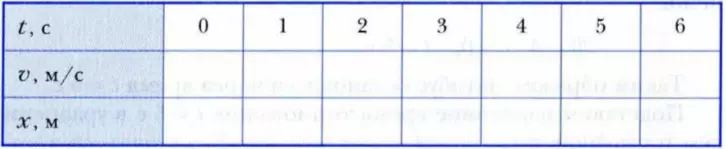
2. Заполните таблицу для тормозящего автобуса, используя условия задачи 2 («торможение»). Ответьте на вопросы: как изменяются со временем: значение скорости; координата тормозящего автобуса?
3. Найдите координату x автомобиля (см. рис. 57) в моменты времени 3, 5 и 8 с, если его начальная координата x0 = 30 м, значение начальной скорости v0 = 10 м/с, а значение ускорения a = 3 м/с 2 .
4. Решите задачу 2 («торможение») в общем виде. Представьте полученный ответ в виде
s = v0 2 / (2 · a).
Проведите анализ полученного ответа. Определите тормозной путь автобуса, если: а) v0 = 16 м/с; б) v0 = 115,2 км/ч.
5. Найдите путь, пройденный автомобилем, движение которого задано в упражнении 3, за промежуток времени от t1 = 2 с до t2 =5 с.
6. Два мотоциклиста, двигавшиеся прямолинейно, начинают одновременно тормозить перед светофором и так же одновременно останавливаются, проехав расстояние s = 100 м. Первый мотоциклист перед торможением двигался со скоростью, имеющей значение v1 = 72 км/ч, второй – со скоростью, имеющей значение v2 = 108 км/ч. Найдите значения ускорений мотоциклистов.
Источник статьи: http://phscs.ru/physics7g/acceleration-braking