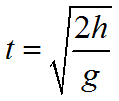Скорость автомобиля выражена формулой

Формулы равномерного и равноускоренного движения

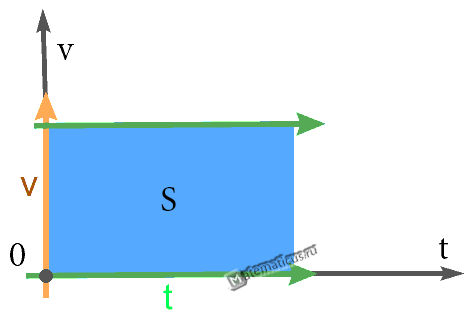
Равномерное движение

Формула скорости движения при равномерном движении: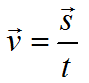

v=const
a=0
v — скорость, м/с
s — перемещение, м
t — время, с
Формула перемещения при равномерном движении: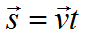

Координата вычисляются через кинематическое уравнение равномерного прямолинейного движения по формуле: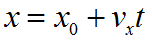

График — Равномерного прямолинейного движения

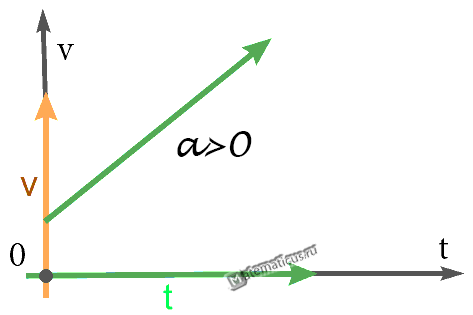
Равноускоренное движение

Формула скорости при равноускоренном движении: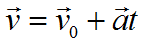

a=const
v₀ — начальная скорость, м/с
a — ускорение, м/с 2
Формула для нахождения перемещения при равноускоренном движении: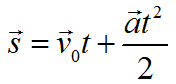

или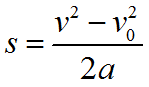

Уравнение равноускоренного движения в проекции на оси координат: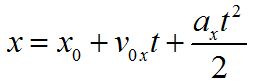

Формула для определения ускорения при равноускоренном прямолинейном движении: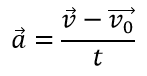

v₀ — начальная скорость, м/с
v — мгновенная скорость, м/с
Формула для определения средней скорости движения: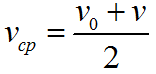

График — Равноускоренное движение при a>0

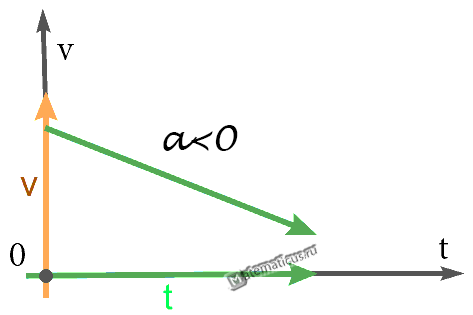
Равнозамедленное движение

Формула скорости при равнозамедленном движении: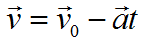

Формула перемещения при равнозамедленном движении: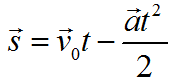

График — Равнозамедленное движение при a 2
Формула для вычисления скорости при свободном падении тела: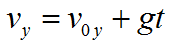

Формула для вычисления перемещения при свободном падении тела: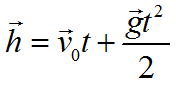


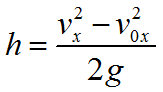
Формула координаты при свободном падении тела: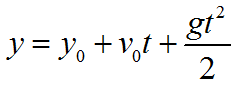

Формула высоты с которой тело свободно падает: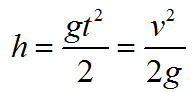

Формула для определения скорости тела в конце свободного падения: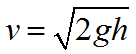

Время свободного падения тела равно:

Источник статьи: http://www.matematicus.ru/fizika/mehanika/formuly-ravnomernogo-i-ravnouskorennogo-dvizheniya

Равномерное прямолинейное движение

Прежде чем начать говорить о равномерном прямолинейном движении необходимо уяснить следующие определения:

• равномерное движение — это движение тела с постоянной (не меняющейся) скоростью. Т. е. скорость при таком движении является константой,
• прямолинейное движение — это такое движение, траектория которого — прямая линия. Другими словами это движение по прямой,
• равномерное прямолинейное движение в таком случае — это движение по прямой с постоянной скоростью. При таком движении тело за равные промежутки времени проходит одинаковые расстояния.

Скорость при прямолинейном движении — величина постоянная. Для того, чтобы найти скорость, необходимо пройденный путь разделить на время, за которое он был пройден.

Формула скорости равномерного прямолинейного движения

V — скорость движения,

S — пройденный путь,

t — время движения

Применительно к равномерному движению можно сказать, что скорость показывает перемещение, которое совершает тело за единицу времени

Из формулы скорости легко выразить формулу для нахождения перемещения тела:

Формула перемещения тела при равномерном прямолинейном движении

V — скорость движения,

S — пройденный путь,

t — время движения

Координату тела при прямолинейном равномерном движении легко найти по формуле:

Координата тела при равномерном прямолинейном движении

x — координата тела в текущий момент времени,

x₀ — координата тела в начальный момент времени,

Источник статьи: http://mnogoformul.ru/ravnomernoe-pryamolineynoe-dvizhenie

Как решать задачи на скорость по физике

Давно планировал начать рубрику для школьников и студентов (а может и не только для них), в которой будет рассказываться о методах решения конкретных задачи и подготовке к экзаменам по физике. Само собой, в этой же рубрике мы поговорим и про егэ по физике, которое пугает ребят больше всего. Пусть рубрика на канале называется # инженер репетитор

Ну а начнем с самого простого — научимся решать задачи на скорость . Эти задачки являются базой для дальнейшего понимания кинематики и динамики, и будут вылезать на протяжении всей механики.

Давайте сначала кратенько вспомним, а что такое скорость?

Кратко про скорость в физике

Скорость в физике — это то насколько быстро изменяется некоторая физическая величина с течением времени. Векторная величина, которая имеет размер и направление.

Например, мы нагреваем комнату. Каждый час система отопления прибавляет в комнате один градус. Значит, скорость прогрева комнаты составляет один градус в час. Или едем мы на велосипеде и за один час проезжаем 20 км. Значит, мы едем со скоростью 20 километров в час.

Вот собственно и всё, что нужно помнить из теории по этому вопросу.

Задачки на скорость обычно сконцентрированы в разделе механики, но вылезают и в других более серьезных разделах физики — скорость света, время течения какой-то реакции, скорость изменения чего-то.

Однако, разобравшись как решать подобные задачи для движения чего-то материального, разобраться и в других разделах проблем не составит. Так или иначе, когда говорят про задачи на скорость, обычно подразумевают именно кинематику и динамику.

Итак, а какие собственно задачи в этой теме бывают и как их решать :)?

Задачи по скорости и их типы

Все задачи из этой темы обычно сводятся к тому, что нужно вытащить скорость из некоторой закономерности . Для этого нужно понимать и примерно помнить формулировки, связанные со скоростью. Их не так много. Не забываем и классические косяки — например привести всё к единой системе СИ.

Самые простые задачки на скорость

Самый простой случай, когда нам известно пройденное расстояние и время, а нужно найти скорость :

S = v * t, значит V = S / t

Находим скорость в м/с или км/ч.

Задачки на «встречу»

Задачки на «встречу». Кто-то едет навстречу кому-то или кто-то кого-то встретил . Обычно такие задачки, с помощью витиеватого условия, пытаются заморочить читателю голову, но суть-то от этого не меняется.

Нам, например, задают граничные условия и указывают, что два мотоциклиста едут по одной дороге в одну сторону и выехали одновременно. Дальше они встретились. Ну и один другого подождал на точке встречи. Один едет 20 минут, а другой едет со скоростью 50 км/ч 60 минут. Найдите скорость первого мотоциклиста. Проблем быть не должно 🙂

Считаем по приведенной выше формуле сколько проехал второй мотоциклист до времени встречи. Из этого расстояния выражаем скорость первого мотоциклиста. Ведь в точке встречи расстояние, которое они проехали было одинаковым. Вот вам и решение.

Вообще, относительно, всей этой тематики, очень полезно освоить процесс рисования чертежей и схем. Нужно сделать доходчивую и понятную схему, которая будет в нужном масштабе отражать все перемещения и их особенность. Это будет залогом практически 100% успеха. Плюс внимательность!

Задачи на скорость в присутствии ускорения

Задачки на равноускоренное движение. Этот тип задач чуть сложнее. В дело вступает ускорение. Что такое ускорение ? Это уже, в свою очередь, быстрота изменения скорости . Обозначается буквой а.

Обычно большая часть величин для решения такой задачи дана или выводится из нехитрой формулы :

V = Vo + аt, где V — скорость, а — ускорение, t — время движения.

В отличие от равномерного движения тело тут перемещается равноускоренно . Т.е. за каждый интервал времени скорость изменяется на одинаковую величину. Это применимо, например, к свободному падению с высоту. Пусть всё тот же мотоциклист едет первый час со скоростью 40 км/ч, а потом разгоняется до 60 км/ч и дальше ускоряется на 20 км/ч каждый час.

Опять-таки, все задачи тут завязаны на «кручу верчу обмануть хочу». И да, на всякий случай отмечу, что все наши рассуждения из пунктов 1 и 2 тут тоже применимы, а ещё ускорение может получиться отрицательным и это не должно вас пугать .

Для решения задач из данной категории вам потребуется внимательно читать условие задачи и включить логику.

Задачки на среднюю скорость

Задачки на среднюю скорость . Тоже очень просто решаются. Что такое средняя скорость — это скорость, полученная как среднее арифметическое от скоростей на каждом из участков.

V средняя = Весь путь (S1+S2+S3+. ) / всё время (t1+t2+t3+. )

Ну а дальше опять комбинаторика :). Подставь-посчитай-вырази. Ловкость рук и внимательность.

Сразу отмечу, что когда мы обсуждаем скорость или ускорение в том разрезе, как мы его видели до сих пор, мы всегда подразумевали именно среднее значение величин . Или не совсем-таки среднее, но условно разбитое на удобное для вычисления количество участков. Усредненное если желаете. В жизни же всё немного иначе.

Речь идёт о том, что если вы представите реальное движение того же несчастного мотоциклиста (или любого другого тела), о котором мы уже много раз вспомнили, он не будет ехать равномерно . Он поедет с рваным ритмом. Там на светофоре постоял. Там перед ямой затормозил. Дальше мотобат его хлопнул, документы проверяет. Бед будет много! И всё это отражается на скорости и как следствие — на ускорении. Это значит, что он действительно может проехать за час свои 50 км, но при этом за полчаса он проедет не 25 км, как мы ожидаем, а всего лишь 10 км, а дальше нагонит разницу .

Если мы высчитываем интегральный или усредненный показатель, нам в принципе-то, фиолетово. Главное, чтобы цифры сошлись. Но если нам нужно определить значение в конкретный момент, то расчёты уже будут неточные. И тут.

задачки, где есть мгновенная скорость

Что такое мгновенная скорость?

Это скорость в конкретный момент времени . Берем мотоциклиста, смотрим на его траекторию. Тыкаем пальцем в любую точку и узнаем, что там скорость пусть 10 км/ч. А через 5 минут уже 70 км/ч. А ещё через 10 минут — опять 10 км/ч. И вовсе не 50 км/ч на всём участке. Или ещё лучше — рисуем график изменения его расстояния в зависимости от времени. По такому графику всегда можно найти мгновенную скорость .

Как подступиться к подобным задачкам?

Для начала мы вспомним, что скорость это — первая производная от функции изменения расстояния по времени. Ведь производная — это и есть скорость изменения величины.

Дальше нам нужна функция, по которой изменялось расстояние. Без неё ничего решить не выйдет. Ведь данных попросту нет.

Исходя из формы кривой у нас будет её уравнение. Дальше нужно его дифференцировать.

Также в этом разделе часто вылезает некоторое дельта R. Что это такое и почему оно в формуле? Это всего лишь то самое значение расстояния (ничтожно малое), пройденного телом, за время стремящееся к нулю.

Ну и да. Для решения задач теперь нужно учитывать, что скорость мгновенная. Больше ничего не меняется .

Задачки на скорость при движении по кривой или окружности

Ещё мы можем столкнуться с понятием угловой скорости .

Начнем с того, что определим, чем вообще ситуация при движении по окружности отличается от ситуации с движением по обычной траектории? По сути дела ничем, кроме того, что путь будет высчитываться относительно окружности — будем считать длину окружности или дуги по известным всем формулам и использовать приведенные ранее зависимости для нахождения скорости.

Это тот самый случай, про который я говорю что учить без понимания бессмысленно. Ведь по сути нам сейчас нужно запомнить только формулы, приведенные раннее, а для криволинейного движения всё высчитаем, опираясь на них и понимая суть вопроса.

Но ко всему этому добавится угловая скорость . Что это? При движении материальной точки по окружности у неё есть линейная скорость, а есть угловая. Смотрим картинку.

Линейная скорость обозначена V, а угловая W (омега). Линейная скорость — это та же скорость, что мы разобрали выше. Она же мгновенная в данном случае. Скорость материальной точки, направленна по касательной к траектории.

Угловая скорость — это то, насколько быстро вращается наш радиус R. Представьте себе часы со стрелками. Стрелка вращается с некоторой скоростью, или — изменяет угол с некоторой скоростью. Вот вам и угловая скорость 🙂 И всё! Считается вот так:

Видите, логика совершенно такая же, как мы рассматривали выше .

Соответственно, в задачках на угловую скорость нужно мыслить аналогично самому первому пункту в нашем гиде. Это просто обычная материальная точка (тело) которая перемещается по окружности . Отличается только траектория ,а в отдельную тему это выделяют попросту для удобства восприятия.

Также, если есть задачка на криволинейное движение, то нужно иметь представление о виде траектории движения тела. Если траектория сложная, то её разбивают на простые геометрические формы и суммируют результаты.

Если нужно сложить скорости

Ещё бывают случаи, когда нужно выполнять сложение скоростей . Например, сложить две скорости разных тел и найти результирующую. Или сложить скорости одного тела.

Опять-таки, бояться таких задачек не нужно!

Вся логика строится из навыка оперировать с векторами.

Скорость — это величина векторная . Значит и зарисовать её можно с помощью вектора определенной длины. Вектора скорости могут быть расположены в одной плоскости или в объеме.

Советую посмотреть вот этот ролик на моем канале

Если вектора скорости находятся в одной плоскости то всё совсем просто. Чаще всего решение сводится к операциям над прямоугольными треугольниками. Бывают и очень простые случаи — векторы скорости вообще направлены вдоль одной прямой. Уже неважно разно направлены они или сонаправлены.

Чуть сложнее ситуация, если векторы скорости расположены в объеме. Там мы приходим к единичным векторам. Ситуация более геморройная, но от того не более сложная.

Я постарался изложить все основы, которые могут помочь вам разобраться с решением задач на скорость. Очень надеюсь, что материал вам поможет.

Писать и разбирать каждую задачку — это довольно объемная штука. Такое нужно рассматривать уже в формате индивидуальных занятий.

Если я забыл осветить что-то в статье или не полностью/непонятно раскрыл теорию вопроса — пожалуйста пишите об этом в комментариях и я дополню статью и отвечу на ваш вопрос :). Давайте вместе сделаем полезный и полный мануал. Ещё можно спросить меня в социальных сетях прямо на страничке https://vk.com/inznan или на лицекниге https://web.facebook.com/inznan

Ну и ответьте пожалуйста на вопрос, нужны ли такие материалы на моем проекте:

Источник статьи: http://zen.yandex.ru/media/inznan/kak-reshat-zadachi-na-skorost-po-fizike-5f684c53c833846a1da39d86