Тангенциальная составляющая скорости автомобиля

Большая Энциклопедия Нефти и Газа

Тангенциальная составляющая — скорость

Тангенциальная составляющая скорости wr оказывает определяющее влияние на закон распределения давления в поперечных сечениях камеры разделения. [2]

Тангенциальная составляющая скорости на больших расстояниях убывает как l / ( r J / V), поэтому ею можно пренебречь. [3]

Тангенциальная составляющая скорости иф зависит в основном только от радиальной координаты г. Это связано, по-видимому, с тем, что при постоянной угловой скорости тангенциальная составляющая скорости частицы прямо пропорциональна радиусу. Отсутствие связей мелсду проекциями скорости частицы и ее угловой координатой р отражает аксиальную симметрию цилиндрического псевдоожиженного слоя. Средне-статистические картины движения частиц в любом меридиональном сечении слоя одинаковы. [4]

Тангенциальная составляющая скорости скольжения согласно табл. 3 совпадает с направлением расходной скорости поверхностных слоев жидкости при отстающем шнеке противоточной центрифуги и опережающем шнеке прямоточной центрифуги. При этом она ускоряет движение поверхностных слоев жидкости вдоль потока и способствует уменьшению его толщины. [5]

Тангенциальная составляющая скорости среды непрерывна при переходе через фронт ударной волны. [6]

В частности, тангенциальная составляющая скорости имеет вид [ 267, стр. [7]

Заметим, что тангенциальная составляющая скорости жидкой фазы на поверхности обращается в нуль ( условие прилипания), а радиальная составляющая ( 5) нет. В процессе кристаллизации на границе раздела фаз существует скачок концентрации примеси. [8]

При сжатии потока его тангенциальная составляющая скорости , по закону сохранения момента количества движения жидкости, увеличивается примерно в отношении диаметра винта к диаметру напорной трубы. Таким образом, если на выходе из нарезок насоса нет никаких устройств ( спирального отвода, направляющего аппарата), раскручивающих поток жидкости, то в напорную трубу жидкость попадает с большой тангенциальной составляющей скорости. Известно, что гидравлическое сопротивление при течении вращающегося потока жидкости через трубу или отверстие может быть в десятки раз больше сопротивления при течении жидкости без вращения. Это явление было установлено уже при первых экспериментах. Были проведены сравнительные испытания одних и тех же рабочих органов со спиралью, направляющим аппаратом и обычной трубой. [9]

С другой стороны, тангенциальная составляющая скорости может претерпевать разрыв только вдоль характеристики. Это ясно из процедуры построения поля скоростей по характеристикам, отправляясь от линии АВ, на которой скорости заданы. Очевидно, что если распределение скоростей на границе имеет разрыв, претерпевать разрыв может только абсолютная величина скорости, но не ее направление, в противном случае произошло бы нарушение сплошности тела. Характеристика, выходящая из точки разрыва граничных условий, будет нести разрыв тангенциальной составляющей скорости. Таким образом, тангенциальная составляющая скорости течения может претерпевать разрыв только на характеристике или на особой линии, служащей огибающей семейства характеристик. [10]

Во-первых, должна быть непрерывной тангенциальная составляющая скорости . Пусть fx ( y t) — малое смещение точек поверхности разрыва в направлении оси х, которое возникает при возмущении стационарного процесса. [11]

Исследования подтвердили вывод, что тангенциальная составляющая скорости несколько увеличивается с уменьшением радиуса вращения, затем начинает убывать. При входе потока в коническую часть ит увеличивается. При повышении давления на входе, за счет увеличения количества подаваемой в гидроциклон жидкости характер эпюр ит по радиусу створа остается неизменным, но увеличиваются абсолютные значения скоростей. [12]

При переходе через линию раздела FO тангенциальная составляющая скорости и испытывает, таким образом, скачок величиной с j / 2, что влечет за собой бесконечную скорость сдвига. По вычисленным значениям и, v строим поле скоростей, продвигаясь последовательно справа налево, пока не достигнем линии АВ; при этом скорости на АВ определяются единственным образом. Далее, в секторе ОАВ находим скорости по данным на отрезках АВ и ОВ. [13]

Следовательно, поверхность, на которой тангенциальная составляющая скорости терпит разрыв, является вихревой пеленой. [14]

Затем, если учесть, что тангенциальная составляющая скорости потока в сопле циклона равна VT и cos а и тогда У. [15]

Источник статьи: http://www.ngpedia.ru/id461503p1.html

Понятия о скорости, тангенциальном и нормальном ускорениях. Формулы

Чтобы уметь решать различные задачи на движение тел по физике, необходимо знать определения физических величин, а также формулы, с помощью которых они связаны. В этой статье будут рассмотрены вопросы, что такое тангенциальная скорость, что такое полное ускорение и какие компоненты его составляют.

Понятие о скорости

Двумя основными величинами кинематики перемещения тел в пространстве являются скорость и ускорение. Скорость описывает быстроту перемещения, поэтому математическая форма записи для нее имеет следующий вид:

Вам будет интересно: Что такое туча? Определение

Здесь l¯ — является вектором перемещения. Иными словами, скорость — это производная по времени от пройденного пути.

Как известно, всякое тело движется по воображаемой линии, которая называется траекторией. Вектор скорости всегда направлен по касательной к этой траектории, в какой бы точке не находилось движущееся тело.

Существует несколько названий величины v¯, если рассматривать ее совместно с траекторией. Так, поскольку направлена она по касательной, то ее называют тангенциальной скоростью. Также о ней могут говорить, как о линейной физической величине в противоположность угловой скорости.

Вычисляется скорость в метрах в секунду в СИ, однако на практике часто пользуются километрами в час.

Понятие об ускорении

В отличие от скорости, которая характеризует быстроту прохождения телом траектории, ускорение — это величина, описывающая быстроту изменения скорости, что математически записывается так:

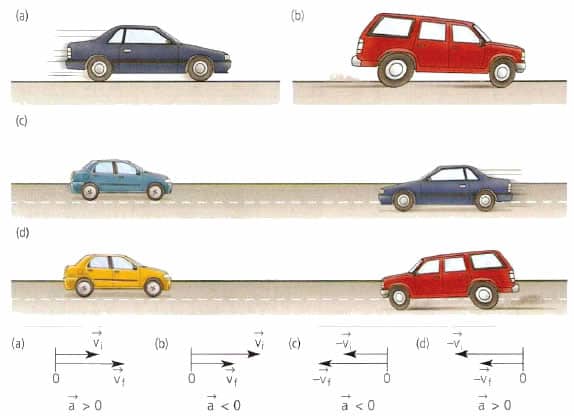
Как и скорость, ускорение — это векторная характеристика. Однако его направление не связано с вектором скорости. Оно определяется изменением направления v¯. Если в процессе движения скорость не изменяет своего вектора, тогда ускорение a¯ будет направлено вдоль той же линии, что и скорость. Такое ускорение называют тангенциальным. Если же скорость будет менять направление, сохраняя при этом абсолютное значение, то ускорение будет направлено к центру кривизны траектории. Оно называется нормальным.

Измеряется ускорение в м/с2. Например, известное всем ускорение свободного падения является тангенциальным при вертикальном подъеме или падении объекта. Его величина вблизи поверхности нашей планеты составляет 9,81 м/с2, то есть за каждую секунду падения скорость тела увеличивается на 9,81 м/с.

Причиной появления ускорения является не скорость, а сила. Если сила F оказывает действие на тело массой m, то она неминуемо создаст ускорение a, которое можно вычислить так:

Эта формула является прямым следствием из второго закона Ньютона.

Полное, нормальное и тангенциальное ускорения

Скорость и ускорение как физические величины были рассмотрены в предыдущих пунктах. Теперь мы подробнее изучим, какие компоненты составляют полное ускорение a¯.

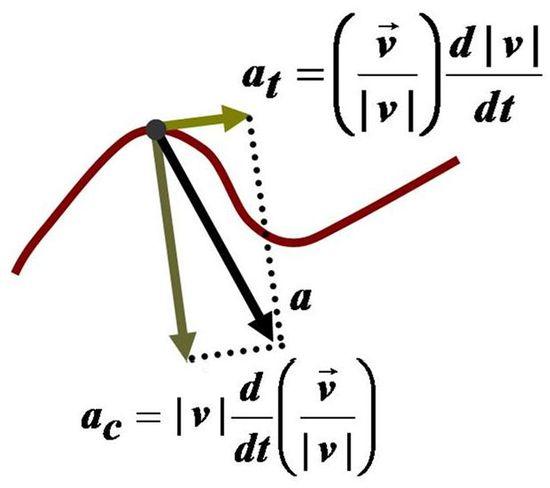
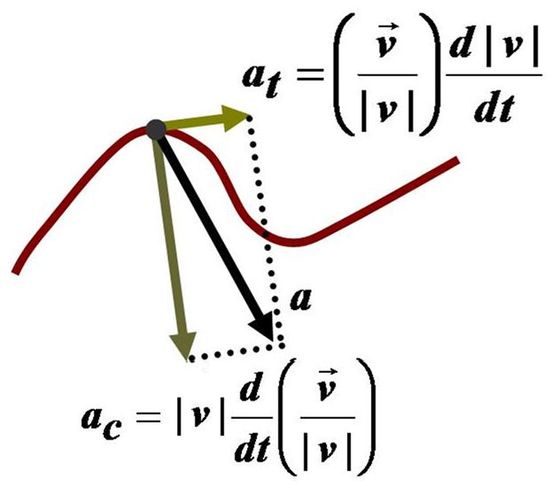
Предположим, что тело движется со скоростью v¯ по криволинейной траектории. Тогда будет справедливо равенство:

Вектор u¯ имеет единичную длину и направлен вдоль касательной линии к траектории. Воспользовавшись таким представлением скорости v¯, получим равенство для полного ускорения:

a¯ = dv¯/dt = d(v*u¯)/dt = dv/dt*u¯ + v*du¯/dt.

Полученное в правом равенстве первое слагаемое называется тангенциальным ускорением. Скорость связана с ним тем фактом, что она количественно определяет изменение абсолютного значения величины v¯, не принимая во внимание ее направление.

Второе слагаемое — это нормальное ускорение. Оно количественно описывает изменение вектора скорости, не принимая во внимание изменение ее модуля.

Если обозначить как at и an тангенциальную и нормальную составляющие полного ускорения a, тогда модуль последнего можно вычислить по формуле:

Связь тангенциального ускорения и скорости

Соответствующую связь описывают кинематические выражения. Например, в случае движения по прямой с постоянным ускорением, которое является тангенциальным (нормальная составляющая равна нулю), справедливы выражения:

В случае движения по окружности с постоянным ускорением эти формулы так же справедливы.

Таким образом, какой бы ни была траектория перемещения тела, тангенциальное ускорение через тангенциальную скорость рассчитывается, как производная по времени от ее модуля, то есть:

Например, если скорость изменяется по закону v = 3*t3 + 4*t, тогда at будет равно:

at = dv/dt = 9*t2 + 4.

Скорость и нормальное ускорение

Запишем в явном виде формулу для нормальной компоненты an, имеем:

an¯ = v*du¯/dt = v*du¯/dl*dl/dt = v2/r*re¯

Где re¯ — единичной длины вектор, который к центру кривизны траектории направлен. Это выражение устанавливает связь тангенциальной скорости и нормального ускорения. Видим, что последнее зависит от модуля v в данный момент времени и от радиуса кривизны r.

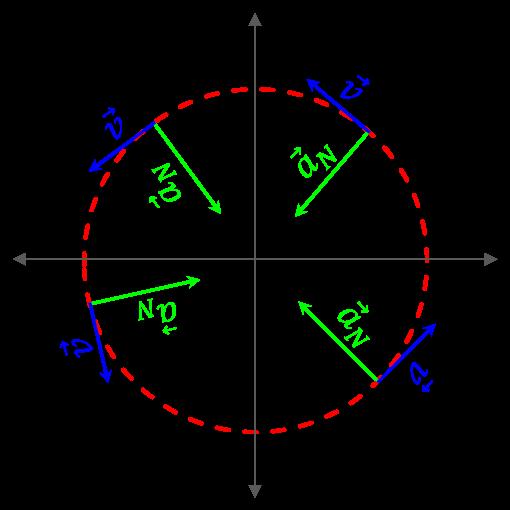
Нормальное ускорение появляется всегда, когда изменяется вектор скорости, однако оно равно нулю, если этот вектор сохраняет направление. Говорить о величине an¯ имеет смысл только тогда, когда кривизна траектории является конечной величиной.

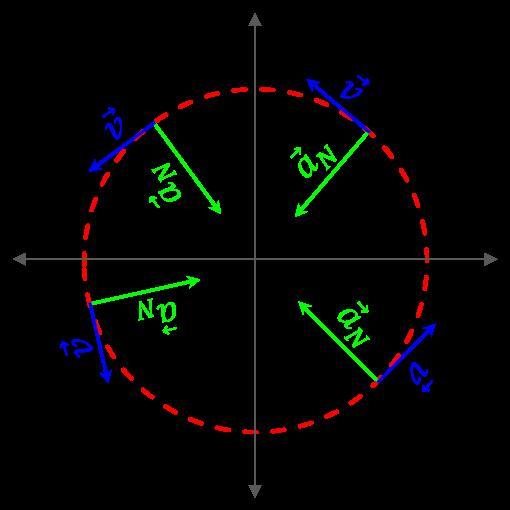
Выше мы отмечали, что при движении по прямой линии нормальное ускорение отсутствует. Однако в природе существует тип траектории, при движении по которой an имеет конечную величину, а at = 0 при |v¯| = const. Этой траекторией является окружность. Например, вращение с постоянной частотой металлического вала, карусели или планеты вокруг собственной оси происходит с постоянным нормальным ускорением an и нулевым тангенциальным ускорением at.

Источник статьи: http://1ku.ru/obrazovanie/52399-ponjatija-o-skorosti-tangencialnom-i-normalnom-uskorenijah-formuly/

Понятия о скорости, тангенциальном и нормальном ускорениях. Формулы

Чтобы уметь решать различные задачи на движение тел по физике, необходимо знать определения физических величин, а также формулы, с помощью которых они связаны. В этой статье будут рассмотрены вопросы, что такое тангенциальная скорость, что такое полное ускорение и какие компоненты его составляют.

Понятие о скорости

Двумя основными величинами кинематики перемещения тел в пространстве являются скорость и ускорение. Скорость описывает быстроту перемещения, поэтому математическая форма записи для нее имеет следующий вид:

Здесь l¯ — является вектором перемещения. Иными словами, скорость — это производная по времени от пройденного пути.

Как известно, всякое тело движется по воображаемой линии, которая называется траекторией. Вектор скорости всегда направлен по касательной к этой траектории, в какой бы точке не находилось движущееся тело.

Существует несколько названий величины v¯, если рассматривать ее совместно с траекторией. Так, поскольку направлена она по касательной, то ее называют тангенциальной скоростью. Также о ней могут говорить, как о линейной физической величине в противоположность угловой скорости.

Вычисляется скорость в метрах в секунду в СИ, однако на практике часто пользуются километрами в час.

Понятие об ускорении

В отличие от скорости, которая характеризует быстроту прохождения телом траектории, ускорение — это величина, описывающая быстроту изменения скорости, что математически записывается так:

Как и скорость, ускорение — это векторная характеристика. Однако его направление не связано с вектором скорости. Оно определяется изменением направления v¯. Если в процессе движения скорость не изменяет своего вектора, тогда ускорение a¯ будет направлено вдоль той же линии, что и скорость. Такое ускорение называют тангенциальным. Если же скорость будет менять направление, сохраняя при этом абсолютное значение, то ускорение будет направлено к центру кривизны траектории. Оно называется нормальным.

Измеряется ускорение в м/с 2 . Например, известное всем ускорение свободного падения является тангенциальным при вертикальном подъеме или падении объекта. Его величина вблизи поверхности нашей планеты составляет 9,81 м/с 2 , то есть за каждую секунду падения скорость тела увеличивается на 9,81 м/с.

Причиной появления ускорения является не скорость, а сила. Если сила F оказывает действие на тело массой m, то она неминуемо создаст ускорение a, которое можно вычислить так:

Эта формула является прямым следствием из второго закона Ньютона.

Полное, нормальное и тангенциальное ускорения

Скорость и ускорение как физические величины были рассмотрены в предыдущих пунктах. Теперь мы подробнее изучим, какие компоненты составляют полное ускорение a¯.

Предположим, что тело движется со скоростью v¯ по криволинейной траектории. Тогда будет справедливо равенство:

Вектор u¯ имеет единичную длину и направлен вдоль касательной линии к траектории. Воспользовавшись таким представлением скорости v¯, получим равенство для полного ускорения:

Полученное в правом равенстве первое слагаемое называется тангенциальным ускорением. Скорость связана с ним тем фактом, что она количественно определяет изменение абсолютного значения величины v¯, не принимая во внимание ее направление.

Второе слагаемое — это нормальное ускорение. Оно количественно описывает изменение вектора скорости, не принимая во внимание изменение ее модуля.

Если обозначить как a_t и a_n тангенциальную и нормальную составляющие полного ускорения a, тогда модуль последнего можно вычислить по формуле:

Связь тангенциального ускорения и скорости

Соответствующую связь описывают кинематические выражения. Например, в случае движения по прямой с постоянным ускорением, которое является тангенциальным (нормальная составляющая равна нулю), справедливы выражения:

В случае движения по окружности с постоянным ускорением эти формулы так же справедливы.

Таким образом, какой бы ни была траектория перемещения тела, тангенциальное ускорение через тангенциальную скорость рассчитывается, как производная по времени от ее модуля, то есть:

Например, если скорость изменяется по закону v = 3*t 3 + 4*t, тогда a_t будет равно:

Скорость и нормальное ускорение

Запишем в явном виде формулу для нормальной компоненты a_n, имеем:

Где r_e¯ — единичной длины вектор, который к центру кривизны траектории направлен. Это выражение устанавливает связь тангенциальной скорости и нормального ускорения. Видим, что последнее зависит от модуля v в данный момент времени и от радиуса кривизны r.

Нормальное ускорение появляется всегда, когда изменяется вектор скорости, однако оно равно нулю, если этот вектор сохраняет направление. Говорить о величине a_n¯ имеет смысл только тогда, когда кривизна траектории является конечной величиной.

Выше мы отмечали, что при движении по прямой линии нормальное ускорение отсутствует. Однако в природе существует тип траектории, при движении по которой a_n имеет конечную величину, а a_t = 0 при |v¯| = const. Этой траекторией является окружность. Например, вращение с постоянной частотой металлического вала, карусели или планеты вокруг собственной оси происходит с постоянным нормальным ускорением a_n и нулевым тангенциальным ускорением a_t.

Источник статьи: http://fb.ru/article/454768/ponyatiya-o-skorosti-tangentsialnom-i-normalnom-uskoreniyah-formulyi