- Все об угловой скорости — определение, единица измерения, методы расчета
- Что такое угловая скорость
- Единица измерения
- Формула угловой скорости
- Зависимость угловой скорости от времени
- Угловая скорость вращения, формула
- Через частоту
- Через радиус
- Как определить направление угловой скорости
- Связь линейной и угловой скорости
- Чему равна мгновенная угловая скорость
- Что такое угловая скорость и как ее рассчитывают?
- Угловая скорость: понятие и формула
- Единицы измерения величины
- Примеры расчета
- Угловая скорость
- Содержание
- Угловая скорость в двухмерном пространстве
- Векторное представление в трёхмерном пространстве
- Тензорное представление
- Единицы измерения
- Свойства
- Связь с конечным поворотом в пространстве
- Примечания
- Комментарии
- Источники
- См. также
- Литература
Все об угловой скорости — определение, единица измерения, методы расчета
Что такое угловая скорость
Угловая скорость (обозначается как \(\omega\) ) — векторная величина, характеризующая скорость и направление изменения угла поворота со временем.
Модуль угловой скорости для вращательного движения совпадает с мгновенной угловой частотой вращения, а направление перпендикулярно плоскости вращения и связано с направлением вращения правилом правого винта.
Единица измерения
В Международной системе единиц (СИ) принятой единицей измерения угловой скорости является радиан в секунду (рад/с)
Формула угловой скорости
Вектор угловой скорости определяется отношением угла поворота \((\varphi)\) к интервалу времени \((\mathcal t)\) , за которое произошел поворот:
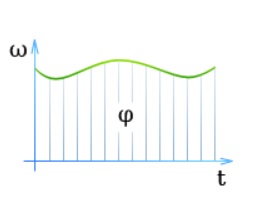
Зависимость угловой скорости от времени
Зависимость \(\varphi \) от \(\mathcal t\) наглядно показана на графике:
Угол, на который повернулось тело, характеризуется площадью под кривой.
Угловая скорость вращения, формула
Через частоту
\(\mathcal n\) — частота вращения \((1/с)\)
\(\pi\) — число Пи ( \(\approx 3,14\) )
\(T \) — период вращения (время, за которое тело совершает один оборот)
Через радиус
\(v\) — линейная скорость(м/с)
\(R\) — радиус окружности (м)
Как определить направление угловой скорости
Направление скорости в физике можно определять двумя способами:
- Правило буравчика. Буравчик имеет правую резьбу (вращательное движение вправо при закручивании). Если вращать буравчик в направлении вращения тела, он будет завинчиваться (или вывинчиваться) в ту сторону, куда направлена угловая скорость.
- Правило правой руки. Представим, что взяли тело в правую руку. Следует направлять и вращать его туда, куда указывают четыре пальца. Отведенный в сторону большой палец покажет направление угловой скорости при этом вращении.
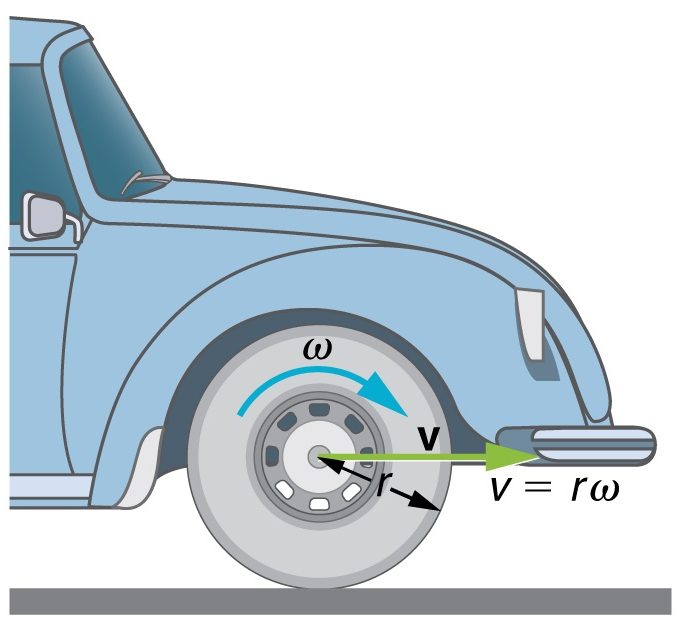
Связь линейной и угловой скорости
Линейная скорость \((v)\) тела, расположенного на расстоянии \(R\) от оси вращения, прямо пропорциональна угловой скорости.
\(R\) — радиус окружности (м)
Чему равна мгновенная угловая скорость
Мгновенную угловую скорость нужно находить как предел, к которому стремится средняя угловая скорость при \(\triangle\mathcal t\rightarrow0\) :
Источник статьи: http://wiki.fenix.help/fizika/vse-ob-uglovoy-skorosti-opredeleniye-yedinitsa-izmereniya-metody-rascheta
Что такое угловая скорость и как ее рассчитывают?
Обычно, когда говорят о перемещении, мы представляем себе объект, который движется по прямой. Скорость такого движения принято называть линейной, и расчёт ее средней величины выполняется просто: достаточно найти отношение пройденного расстояния к времени, за которое оно было телом преодолено. Если же объект перемещается по окружности, то в этом случае уже определяется не линейная, а угловая скорость. Что это за величина и как ее рассчитывают? Об этом как раз и пойдет разговор в данной статье.
Угловая скорость: понятие и формула
Когда материальная точка движется по окружности, быстроту ее перемещения можно характеризовать величиной угла поворота радиуса, который соединяет движущийся объект с центром данной окружности. Понятно, что эта величина в зависимости от времени постоянно меняется. Быстрота, с которой этот процесс происходит, и есть не что иное, как угловая скорость. Другими словами, это отношение величины отклонения радиус-вектора объекта к промежутку времени, которое потребовалось объекту на совершение такого поворота. Формула угловой скорости (1) может быть записана в таком виде:
φ – угол поворота радиуса,
t – период времени вращения.
Единицы измерения величины
В международной системе общепринятых единиц (СИ) для характеристики поворотов принято использовать радианы. Поэтому 1 рад/с – основная единица, которая используется в расчетах угловой скорости. В то же время никто не запрещает применять градусы (напомним, что один радиан равен 180/пи, или 57˚18’). Также угловая скорость может выражаться в числе оборотов за минуту или за секунду. Если перемещение по окружности происходит равномерно, то данная величина может быть найдена по формуле (2):
где n – частота вращения.
В противном случае подобно тому, как это делают для обычной скорости, рассчитывают среднюю, или мгновенную угловую скорость. Следует отметить, что рассматриваемая величина является векторной. Для определения ее направления обычно используют правило буравчика, которое часто применяется в физике. Вектор угловой скорости направлен в ту же сторону, в которую происходит поступательное движение винта с правой резьбой. Другими словами, он устремлен вдоль оси, вокруг которой вращается тело, в ту сторону, откуда вращение видно происходящим против движения часовой стрелки.
Примеры расчета
Предположим, требуется определить, чему равна линейная и угловая скорость колеса, если известно, что его диаметр равен одному метру, а угол вращения изменяется в соответствии с законом φ=7t. Воспользуемся нашей первой формулой:
w = φ / t = 7t / t = 7 с -1 .
Это и будет искомая угловая скорость. Теперь перейдем к поиску привычной нам быстроты перемещения. Как известно, v = s / t. Учитывая, что s в нашем случае – это длина окружности колеса (l =2π*r), а 2π — один полный оборот, получается следующее:
v = 2π*r / t = w * r = 7 * 0.5 = 3.5 м/с
Вот еще одна задачка на эту тему. Известно, что радиус Земли на экваторе равен 6370 километров. Требуется определить линейную и угловую быстроту движения точек, находящихся на этой параллели, которое возникает в результате вращения нашей планеты вокруг своей оси. В данном случае нам понадобится вторая формула:
w = 2π*n = 2*3,14 *(1/(24*3600)) = 7,268 *10 -5 рад/с.
Осталось выяснить, чему равна линейная скорость: v = w*r = 7,268 *10 -5 *6370 * 1000 = 463 м/с.
Источник статьи: http://fb.ru/article/126885/chto-takoe-uglovaya-skorost-i-kak-ee-rasschityivayut
Угловая скорость
| Угловая скорость | |
ω <\displaystyle \omega >  | |
| Размерность | T −1 |
|---|---|
| Единицы измерения | |
| СИ | рад/с |
| СГС | рад/с |
| Другие единицы | градус/с об/с об/мин |
Углова́я ско́рость — величина, характеризующая скорость вращения материальной точки вокруг центра вращения. Для вращения в двухмерном пространстве угловая скорость выражается числом, в трёхмерном пространстве представляется псевдовектором (аксиальным вектором), а в общем случае — кососимметрическим тензором [1] .
Содержание
Угловая скорость в двухмерном пространстве
Векторное представление в трёхмерном пространстве
В трёхмерном пространстве вектор угловой скорости по величине равен углу поворота точки вокруг центра вращения за единицу времени:
ω = d φ d t , <\displaystyle \omega =<\frac

а направлен по оси вращения согласно правилу буравчика, то есть в ту сторону, в которую ввинчивался бы буравчик или винт с правой резьбой, если бы вращался в эту сторону. Другой мнемонический подход для запоминания взаимной связи между направлением вращения и направлением вектора угловой скорости состоит в том, что для условного наблюдателя, находящегося на конце вектора угловой скорости, выходящего из центра вращения, само вращение выглядит происходящим против часовой стрелки.
Угловая скорость является аксиальным вектором (псевдовектором). При отражении осей системы координат компоненты обычного вектора (например, радиус-вектора точки) меняют знак. В то же время компоненты псевдовектора (в частности, угловой скорости) при таком преобразовании координат остаются прежними.
Тензорное представление
Единицы измерения
Единица измерения угловой скорости, принятая в Международной системе единиц (СИ) и в системах СГС и МКГСС, — радиан в секунду (русское обозначение: рад/с, международное: rad/s) [2] [Комм 1] . В технике также используются обороты в секунду, намного реже — градусы, минуты, секунды дуги в секунду, грады в секунду. Часто в технике используют обороты в минуту — это идёт с тех времён, когда частоту вращения тихоходных паровых машин определяли просто на глаз, подсчитывая число оборотов за единицу времени.
Свойства
Вектор мгновенной скорости любой точки абсолютно твёрдого тела, вращающегося с угловой скоростью ω → <\displaystyle <\vec <\omega >>> 
v → = [ ω → , r → ] , <\displaystyle <\vec
где r → <\displaystyle <\vec 


- В случае плоского вращения, то есть когда все векторы скоростей точек тела всегда лежат в одной плоскости («плоскости вращения»), угловая скорость тела всегда перпендикулярна этой плоскости, и по сути — если плоскость вращения заведомо известна — может быть заменена скаляром — проекцией на ось вращения, то есть на прямую, ортогональную плоскости вращения. В этом случае кинематика вращения сильно упрощается. Однако в общем случае угловая скорость может менять со временем направление в трёхмерном пространстве, и такая упрощенная картина не работает.
- Движение с постоянным вектором угловой скорости называется равномерным вращательным движением (в этом случае угловое ускорение равно нулю). Равномерное вращение является частным случаем плоского вращения.
- Производная угловой скорости по времени есть угловое ускорение.
- Угловая скорость (рассматриваемая как свободный вектор) одинакова во всех инерциальных системах отсчёта, отличающихся положением начала отсчёта и скоростью его движения, но двигающихся равномерно прямолинейно и поступательно друг относительно друга. Однако в этих инерциальных системах отсчёта может различаться положение оси или центра вращения одного и того же конкретного тела в один и тот же момент времени (то есть будет различной «точка приложения» угловой скорости).
- В случае движения точки в трёхмерном пространстве можно написать выражение для угловой скорости этой точки относительно выбранного начала координат:
ω → = r → × v → ( r → , r → ) , <\displaystyle <\vec <\omega >>=<\frac <<\vec 






- В случае равномерного вращательного движения (то есть движения с постоянным вектором угловой скорости) абсолютно твёрдого тела декартовы координаты точек вращающегося так тела совершают гармонические колебания с угловой (циклической) частотой, равной модулю вектора угловой скорости.
- При измерении угловой скорости в оборотах в секунду (об/с) модуль угловой скорости равномерного вращательного движения совпадает с частотой вращенияf , измеренной в герцах (Гц), то есть в таких единицах ω = f . <\displaystyle \omega =f.>
В случае использования обычной физической единицы угловой скорости — радианов в секунду — модуль угловой скорости численно связан с частотой вращения так: ω = 2 π f . <\displaystyle \omega =<2\pi f>.>
Наконец, при использовании градусов в секунду численная связь с частотой вращения будет: ω = 360 ∘ f . <\displaystyle \omega =<360^<\circ >f>.>
Связь с конечным поворотом в пространстве
- Пусть поворот, изменяющийся во времени, задан величиной угла θ ( t ) <\displaystyle \;\theta (t)>
и ортом оси конечного поворота в пространстве n → ( t ) . <\displaystyle <\vec
>(t).> Тогда угловая скорость, соответствующая этому повороту, равна
ω → = n → θ ˙ + n → ˙ sin θ + n → × n → ˙ ( 1 − cos θ ) . <\displaystyle <\vec <\omega >>=<\vec
- Если поворот задан матрицей поворота T i j = n i n j + ( δ i j − n i n j ) cos θ − n k ϵ i j k sin θ , <\displaystyle T_
=n_n_ +(\delta _ -n_n_ )\cos \theta -n_ \epsilon _ \sin \theta ,> где δ i j <\displaystyle \;\delta _
> — символ Кронекера, ε i j k <\displaystyle \varepsilon _
> — символ Леви-Чивиты (суммирование ведётся по правилу Эйнштейна от 1 до 3), выражение для элементов которой через θ <\displaystyle \;\theta >
и n → <\displaystyle <\vec
>> могут быть получены, например, с помощью формулы Родрига, то угловая скорость равна
ω i = 1 2 ε i j k T j n T ˙ k n . <\displaystyle \omega _=<\frac <1><2>>\varepsilon _
- Если для описания поворота используется кватернион, выражаемый через угол θ <\displaystyle \;\theta >
и орт оси поворота n → <\displaystyle <\vec
>> как q = ( cos ( θ / 2 ) , n → sin ( θ / 2 ) ) , <\displaystyle q=<\bigl (>\cos(\theta /2),<\vec
>\sin(\theta /2)<\bigr )>,> то угловая скорость находится из выражения ( 0 , ω → ) = 2 q ˙ q ¯ . <\displaystyle \left(0,<\vec <\omega >>\right)=2\,<\dot
>\,<\overline
>.>
- В случае, когда поворот описывается с помощью вектора V → = n → tg ( θ / 4 ) , <\displaystyle <\vec
>=<\vec >\operatorname (\theta /4),> изменяющегося во времени, обозначим W → = d V → / d t ( W i = d V i / d t ) , <\displaystyle <\vec
>=d<\vec >/dt\ <\bigl (>W_=dV_/dt<\bigr )>,> а также T i j 1 / 2 = n i n j + ( δ i j − n i n j ) cos ( θ / 2 ) − n k ϵ i j k sin ( θ / 2 ) <\displaystyle T_
^<1>=n_n_ +(\delta _ -n_n_ )\cos(\theta /2)-n_ \epsilon _ \sin(\theta /2)> — матрица половинного поворота ( T i j 1 / 2 T j k 1 / 2 = T i k ) , <\displaystyle \;<\bigl (>T_
^<1>T_ ^<1>=T_ <\bigr )>,> V 2 <\displaystyle \;V^<2>>
— квадрат модуля вектора V → . <\displaystyle <\vec
>.> Тогда угловая скорость:
ω i = 4 T i j 1 / 2 W j 1 + V 2 . <\displaystyle \omega _=<\frac <4T_
Примечания
Комментарии
- ↑Плоский угол, определяемый как отношение длины дуги окружности, заключённой между двумя радиусами, к длине радиуса, безразмерен, поэтому единицей измерения плоских углов является число «один», а единицей измерения угловой скорости в системе СИ — с −1 . Однако, в случае плоских углов единице «один» присвоено специальное наименование «радиан» для того, чтобы в каждом конкретном случае облегчить понимание того, какая именно физическая величина имеется в виду [3] .
Источники
- ↑Ишлинский А. Ю. Классическая механика и силы инерции / Отв. ред. Б. В. Раушенбах. — М. : «Наука», 1987. — С. 239.
- ↑Деньгуб В. М. , Смирнов В. Г. Единицы величин. Словарь-справочник. — М. : Издательство стандартов, 1990. — С. 98. — 240 с. — ISBN 5-7050-0118-5.
- ↑Units for dimensionless quantities, also called quantities of dimension one (англ.) . SI Brochure: The International System of Units (SI). Международное бюро мер и весов (2006; обновлено в 2014). Проверено 29 января 2016.
См. также
Литература
- Лурье А. И. Аналитическая механика. — М. : ГИФМЛ, 1961. — С. 100-136. — 824 с.
Что такое wiki2.info Вики является главным информационным ресурсом в интернете. Она открыта для любого пользователя. Вики это библиотека, которая является общественной и многоязычной.
Основа этой страницы находится в Википедии. Текст доступен по лицензии CC BY-SA 3.0 Unported License.
Wikipedia® — зарегистрированный товарный знак организации Wikimedia Foundation, Inc. wiki2.info является независимой компанией и не аффилирована с Фондом Викимедиа (Wikimedia Foundation).
Источник статьи: http://wiki2.info/%D0%A3%D0%B3%D0%BB%D0%BE%D0%B2%D0%B0%D1%8F_%D1%81%D0%BA%D0%BE%D1%80%D0%BE%D1%81%D1%82%D1%8C