. для школьных учителей .
Как теперь смотреь флэш-файлы!








Примеры решения задач по теме «Равномерное прямолинейное движение»
«Физика — 10 класс»
При решении задач по данной теме необходимо прежде всего выбрать тело отсчёта и связать с ним систему координат. В данном случае движение происходит по прямой, поэтому для его описания достаточна одна ось, например ось ОХ. Выбрав начало отсчёта, записываем уравнения движения.
Задача I.
Определите модуль и направление скорости точки, если при равномерном движении вдоль оси ОХ её координата за время t1 = 4 с изменилась от х1 = 5 м до х2 = -3 м.
Модуль и направление вектора можно найти по его проекциям на оси координат. Так как точка движется равномерно, то проекцию её скорости на ось ОХ найдём по формуле
Отрицательный знак проекции скорости означает, что скорость точки направлена противоположно положительному направлению оси ОХ. Модуль скорости υ = |υх| = |-2 м/с| = 2 м/с.
Задача 2.
Из пунктов А и В, расстояние между которыми вдоль прямого шоссе l0 = 20 км, одновременно навстречу друг другу начали равномерно двигаться два автомобиля. Скорость первого автомобиля υ1 = 50 км/ч, а скорость второго автомобиля υ2 = 60 км/ч. Определите положение автомобилей относительно пункта А спустя время t = 0,5 ч после начала движения и расстояние I между автомобилями в этот момент времени. Определите пути s1 и s2, пройденные каждым автомобилем за время t.
Примем пункт А за начало координат и направим координатную ось ОХ в сторону пункта В (рис. 1.14). Движение автомобилей будет описываться уравнениями
Так как первый автомобиль движется в положительном направлении оси ОХ, а второй — в отрицательном, то υ1x = υ1, υ2x = —υ2. В соответствии с выбором начала координат х01 = 0, х02 = l0. Поэтому спустя время t
x1 = υ1t = 50 км/ч • 0,5 ч = 25 км;
х2 = l0 — υ2t = 20 км — 60 км/ч • 0,5 ч = -10 км.
Первый автомобиль будет находиться в точке С на расстоянии 25 км от пункта А справа, а второй — в точке D на расстоянии 10 км слева. Расстояние между автомобилями будет равно модулю разности их координат: l = |х2 — x1| = |—10 км — 25 км| = 35 км. Пройденные пути равны:
s1 = υ1t = 50 км/ч • 0,5 ч = 25 км,
s2 = υ2t = 60 км/ч • 0,5 ч = 30 км.
Задача 3.
Из пункта А в пункт В выезжает первый автомобиль со скоростью υ1 Спустя время t0 из пункта В в том же направлении со скоростью υ2 выезжает второй автомобиль. Расстояние между пунктами A и В равно l. Определите координату места встречи автомобилей относительно пункта В и время от момента отправления первого автомобиля, через которое они встретятся.
Примем пункт А за начало координат и направим координатную ось ОХ в сторону пункта В (рис. 1.15). Движение автомобилей будет описываться уравнениями
В момент встречи координаты автомобилей равны: х1 = х2 = хв. Тогда υ1tв = l + υ2( tв — t0) и время до встречи
Очевидно, что решение имеет смысл при υ1 > υ2 и l > υ2t0 или при υ1
За время, равное 4 с, изменение координаты первой точки: Δx1 = 4 — 2 (м) = 2 м, второй точки: Δх2 = 4 — 0 (м) = 4 м.
1) Скорости точек определим по формуле 
2) Время встречи — это момент времени, когда координаты точек равны. Очевидно, что tв = 4 с.
3) Пути, пройденные точками, равны их перемещениям и равны изменениям их координат за время до встречи: s1 = Δх1= 2 м, s2 = Δх2 = 4 м.
Уравнения движения для обеих точек имеют вид х = х0 + υxt, где х0 = x01 = 2 м, υ1x = 0,5 м/с — для первой точки; х0 = х02 = 0, υ2x = 1 м/с — для второй точки.
Источник: «Физика — 10 класс», 2014, учебник Мякишев, Буховцев, Сотский
Кинематика — Физика, учебник для 10 класса — Класс!ная физика
Источник статьи: http://class-fizika.ru/10_a6.html
Задачи по физике прямолинейное движение автомобиля
Задача № 1. Ласточка летит со скоростью 36 км/ч. Какой путь она преодолеет за 0,5 ч?
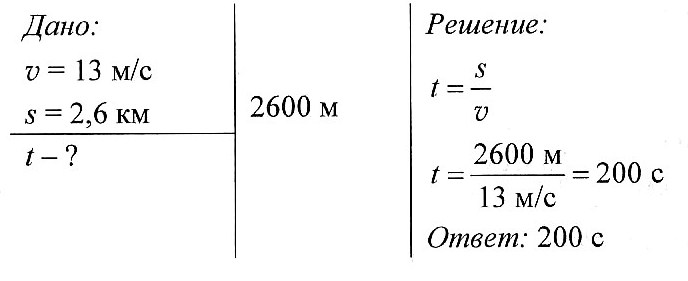
Задача № 1. Конькобежец может развивать скорость до 13 м/с. За какое время он пробежит дистанцию длиной 2,6 км?
Задача № 3. Автомобиль «Чайка» развивает скорость до 160 км/ч, а почтовый голубь — до 16 м/с. Сможет ли голубь обогнать автомобиль?
Решение. Чтобы сравнить скорости движения тел, надо перевести их в одинаковые единицы измерения. Перевод скорости из одних единиц в другие выполняют следующим образом. 160 км = 160000 м, 1 ч = 3600 с. Следовательно, за 1 с автомобиль пройдет путь 160000 : 3600 = 44 (м), значит: 
Ответ: Голубь не обгонит автомобиль, так как 16 м/с
Задача № 4. Вдоль дороги навстречу друг другу летят скворец и комнатная муха. На рисунке представлены графики движения скворца (I) и мухи (II). Пользуясь графиком, определите:
1) Каковы скорости движения скворца и мухи?
2) Через сколько секунд после начала движения они встретятся?
3) Какое расстояние они пролетят до места встречи?
Решение.
1. Скорость движения скворца определим по формуле v=S/t. Выберем на графике произвольное время и определим, какое расстояние за это время пролетел скворец. Видно, что за 5 с скворец пролетел 100 м. Тогда 
Аналогично найдем скорость движения мухи:

2. Точка А (точка пересечения графиков движения) соответствует моменту встречи. Скворец и муха встретятся через 4 секунды.
3. Скворец до места встречи пролетит расстояние SI = 80 м. Муха пролетит расстояние SII = 100 м — 80 м = 20 м.
Ответ: 1) скворец 20 м/с, муха 5 м/с, 2) через 4 с, 3) скворец 80 м, муха 20 м
Задача № 5. Определите среднюю скорость движения плота, если за 20 минут он переместился на 900 м. Скорость выразить в км/ч.
Ответ: Средняя скорость плота 2,7 км/ч.
Задача № 6. Стоящий на эскалаторе человек поднимается за 2 мин, а бегущий по эскалатору — за 40 с. За какое время этот человек поднимется по неподвижному эскалатору?
ОТВЕТ: 1 мин.
Задача № 7. Моторная лодка за 3 ч проходит расстояние от города до поселка, расположенного ниже по течению реки. Сколько времени займет обратный путь, если скорость движения лодки относительно воды в 4 раза больше скорости течения?
ОТВЕТ: 5 ч.
Задача № 8 (повышенной сложности). Рыбак плыл по реке на лодке, зацепил шляпой за мост, и она свалилась в воду. Через час рыбак спохватился, повернул обратно и подобрал шляпу на 4 км ниже моста. Какова скорость течения? Скорость лодки относительно воды оставалась неизменной по модулю.
ОТВЕТ: 2 км/ч.
Задача № 9 (олимпиадного уровня). Из городов А и Б навстречу друг другу по прямому шоссе одновременно выехали два велосипедиста. Скорость первого 10 км/ч, скорость второго 15 км/ч. Одновременно с велосипедистами из города А вылетела ласточка. Она долетает до второго велосипедиста, разворачивается, Долетает до первого велосипедиста и летает так между ними до тех пор, пока велосипедисты не встретятся. Какой путь пролетела ласточка, если скорость ее движения 50 км/ч, а расстояние между городами 100 км? Временем разворота ласточки можно пренебречь.
ОТВЕТ: 200 км.
Алгоритм решения задач на движение
При решении других задач прямолинейного равномерного движения в общем виде нужно придерживаться следующего алгоритма: 1) выбрать систему отсчёта; 2-3) определить начальные координаты и значения скоростей движения тел в этой системе отсчёта; 4) записать зависимости координат тел от времени; 5) записать в виде уравнения условие задачи; 6) объединить уравнения; 7) решить эти уравнения; 8) провести анализ полученного результата (после чего выяснить, имеет ли полученный результат физический смысл); 9) если в условии задачи даны числовые значения, необходимо подставить их в полученное выражение и получить числовой ответ.
Анализ полученного результата заключается в исследовании зависимости искомой величины от входящих в ответ величин.
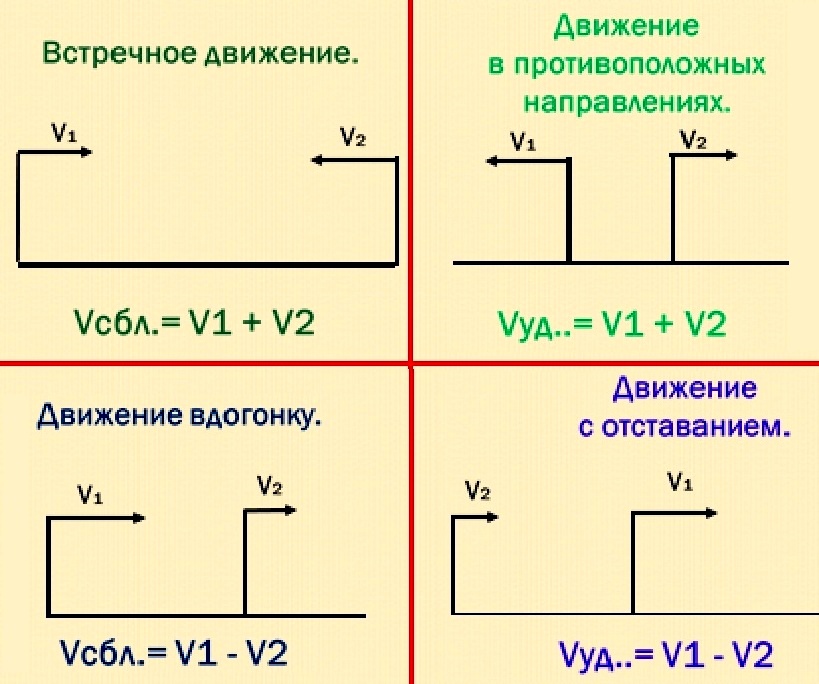
Не стоит забывать и про направление движения в зависимости от типа задачи (встреча, погоня, обгон, отставание)
Конспект урока «Задачи на движение с решением».
Источник статьи: http://uchitel.pro/%D0%B7%D0%B0%D0%B4%D0%B0%D1%87%D0%B8-%D0%BD%D0%B0-%D0%B4%D0%B2%D0%B8%D0%B6%D0%B5%D0%BD%D0%B8%D0%B5/
Прямолинейное равномерное движение задачи по физике
Для дошкольников и учеников 1-11 классов
Рекордно низкий оргвзнос 25 Р.
Решение задач «Прямолинейное равномерное движение»
1. Прямолинейное движение
Прямолинейное движение тела — это движение, при котором тело движется по прямой линии в данной системе отсчёта.
Чтобы описать прямолинейное движение в выбранной системе отсчёта, необходимо в момент начала движения включить часы и измерять координату тела в различные моменты времени. Результаты измерений представляют в виде таблицы (табличный способ описания движения) или графика движения в осях: время — координата (графический способ описания движения).
Если известна графическая зависимость координаты тела от времени в виде непрерывной линии , то движение тела описано полностью, т. е. можно:
Определить координату тела в любой момент времени движения (ответить на вопрос «где?»).
Определить момент времени , в который тело имело заданную координату (ответить на вопрос «когда?»).
Охарактеризовать движение тела (указать, покоилось ли тело, двигалось ли в положительном или отрицательном направлении координатной оси, как быстро изменялась его координата с течением времени).
2. Равномерное движение
Прямолинейное движение тела называют равномерным, если тело за любые равные промежутки времени проходит равные расстояния в одном и том же направлении. Изменением координаты тела за промежуток времени от момента t 1 до момента t 2 называют разность х 2 — х 1 между конечным и начальным значениями координаты.
Прямолинейное равномерное движение характеризуется тем, что изменение координаты тела за единицу времени (её обычно обозначают латинской буквой v) есть величина постоянная. График зависимости координаты х тела от времени t для такого движения представляет собой прямую линию . При этом зависимость координаты тела от времени имеет вид:
x = х 0 + v • t,
где х 0 — начальная координата тела, t — момент времени после начала движения, v — постоянная величина, равная изменению координаты тела за единицу времени, х — координата тела в момент времени t.
3. Скорость прямолинейного равномерного движения
Если тело движется равномерно прямолинейно, то физическую величину v , численно равную изменению его координаты за единицу времени, называют значением скорости равномерного прямолинейного движения. В СИ единица скорости — метр в секунду (м/с) .
Скорость — векторная величина, которая характеризуется не только своим модулем, но и направлением. Если значение скорости положительно, то скорость направлена в положительном направлении оси X. Если же значение скорости отрицательно, то скорость направлена в отрицательном направлении оси X.
Задача № 1. Ласточка летит со скоростью 36 км/ч. Какой путь она преодолеет за 0,5 ч?
Задача № 1. Конькобежец может развивать скорость до 13 м/с. За какое время он пробежит дистанцию длиной 2,6 км?
Задача № 3. Автомобиль «Чайка» развивает скорость до 160 км/ч, а почтовый голубь — до 16 м/с. Сможет ли голубь обогнать автомобиль?
Решение. Чтобы сравнить скорости движения тел, надо перевести их в одинаковые единицы измерения. Перевод скорости из одних единиц в другие выполняют следующим образом. 160 км = 160000 м, 1 ч = 3600 с. Следовательно, за 1 с автомобиль пройдет путь 160000 : 3600 = 44 (м) , значит:

Ответ: Голубь не обгонит автомобиль, так как 16 м/с .
Задача № 4. Вдоль дороги навстречу друг другу летят скворец и комнатная муха. На рисунке представлены графики движения скворца (I) и мухи (II). Пользуясь графиком, определите:
1) Каковы скорости движения скворца и мухи?
2) Через сколько секунд после начала движения они встретятся?
3) Какое расстояние они пролетят до места встречи?
Решение.
1. Скорость движения скворца определим по формуле v=S/t. Выберем на графике произвольное время и определим, какое расстояние за это время пролетел скворец. Видно, что за 5 с скворец пролетел 100 м . Тогда
Аналогично найдем скорость движения мухи:
2. Точка А (точка пересечения графиков движения) соответствует моменту встречи. Скворец и муха встретятся через 4 секунды .
3. Скворец до места встречи пролетит расстояние S I = 80 м . Муха пролетит расстояние S II = 100 м — 80 м = 20 м .
Ответ: 1) скворец 20 м/с, муха 5 м/с, 2) через 4 с, 3) скворец 80 м, муха 20 м
Задача № 5. Определите среднюю скорость движения плота, если за 20 минут он переместился на 900 м. Скорость выразить в км/ч.
Ответ : Средняя скорость плота 2,7 км/ч.
Задача № 6. Стоящий на эскалаторе человек поднимается за 2 мин, а бегущий по эскалатору — за 40 с. За какое время этот человек поднимется по неподвижному эскалатору?
Решение. Стоящий на эскалаторе человек за 1 мин перемещается на половину длины эскалатора, а бегущий — перемещается на полторы длины эскалатора. Следовательно, идущий по неподвижному эскалатору человек за 1 мин перемещается как раз на длину эскалатора.
Задача № 7. Моторная лодка за 3 ч проходит расстояние от города до поселка, расположенного ниже по течению реки. Сколько времени займет обратный путь, если скорость движения лодки относительно воды в 4 раза больше скорости течения?
Решение. Обозначим скорость течения v . При движении по течению скорость лодки относительно берега равна 5v , а при движении против течения ее скорость равна 3v . Следовательно, время движения против течения в 5/3 раза больше, чем время движения по течению.
Рыбак плыл по реке на лодке, зацепил шляпой за мост, и она свалилась в воду. Через час рыбак спохватился, повернул обратно и подобрал шляпу на 4 км ниже моста. Какова скорость течения? Скорость лодки относительно воды оставалась неизменной по модулю.
Решение. Удобно рассматривать движение шляпы и лодки относительно воды, потому что относительно воды шляпа неподвижна, а скорость лодки, когда она плывет от шляпы и к шляпе, по модулю одна и та же — так, как это было бы в озере. Следовательно, после поворота рыбак плыл к шляпе тоже 1 ч , т. е. он подобрал шляпу через 2 ч после того, как уронил ее. По условию за это время шляпа проплыла по течению 4 км , откуда следует, что скорость течения 2 км/ч .
Задача № 9 (олимпиадного уровня). Из городов А и Б навстречу друг другу по прямому шоссе одновременно выехали два велосипедиста. Скорость первого 10 км/ч, скорость второго 15 км/ч. Одновременно с велосипедистами из города А вылетела ласточка. Она долетает до второго велосипедиста, разворачивается, Долетает до первого велосипедиста и летает так между ними до тех пор, пока велосипедисты не встретятся. Какой путь пролетела ласточка, если скорость ее движения 50 км/ч, а расстояние между городами 100 км? Временем разворота ласточки можно пренебречь.
Решение. Расстояние между велосипедистами каждый час уменьшается на 25 км . Поскольку начальное расстояние между ними 100 км , они встретятся через 4 ч. Все это время ласточка будет летать со скоростью 50 км/ч , следовательно, ее путь составит 200 км.
Источник статьи: http://infourok.ru/pryamolinejnoe-ravnomernoe-dvizhenie-zadachi-po-fizike-4369429.html