Зависимость силы тяги от скорости автомобиля

Содержание

Как найти силу тяги
Что такое сила тяги
Действие силы тяги
Её прекращение
1 закон Ньютона о действии
Состояние ускорения после воздействия силы тяги
Формулы для определения силы тяги
Какое условие должно соблюдаться
Формула через мощность
Измерение и обозначение силы тяги
Как определить силу тяги двигателя. Примеры решения задач
Зависимость силы тяги от скорости
Зависимость силы тяги от скорости

Как найти силу тяги

Что такое сила тяги

Сила тяги — сила, прикладываемая к телу для поддержания его в постоянном движении.

Действие силы тяги

Множество сил, действующих на движущийся объект, для упрощения вычислений делят на две группы: силу тяги и силы сопротивления.

Её прекращение

Когда действие силы тяги прекращается, движущееся тело замедляется и постепенно останавливается, так как на него воздействуют силы, мешающие продолжать двигаться, например, трение.

1 закон Ньютона о действии

Согласно этому закону в формулировке самого Ньютона, любое тело остается в покое или равномерно движется по прямой, пока на него не воздействуют силы, заставляющие его изменить это состояние.

В современной физике в формулировку внесены уточнения:

закон применим только в системах отсчета, называемых инерциальными;
тело может вращаться на месте, не находясь под воздействием внешних сил, поэтому вместо термина «тело» следует использовать термин «материальная точка».

Чтобы переместить неподвижный предмет, на него должна воздействовать некая сила. Чтобы изменить скорость движения предмета, также необходимо воздействие силы, замедляющей его или ускоряющей. Так как предметы обладают разной массой и соответственно разной инертностью, силы, достаточные для эффективного воздействия, тоже будут различаться.

Состояние ускорения после воздействия силы тяги

Когда движение равномерное, сила тяги и сила трения совершают одинаковую работу, уравновешивая друг друга. Воздействие силы на тело в направлении движения придает ему ускорение. Если направить ту же силу в противоположном направлении, она замедлит движение тела, что можно назвать отрицательным ускорением.

Формулы для определения силы тяги

Согласно второму закону Ньютона, сумма сил, воздействующих на движущееся тело, равна массе \(m\) , умноженной на ускорение \(a\) . Универсальной формулы, подходящей для любого сочетания сил, не существует. Чаще всего силу тяги находят с помощью общей формулы \( F_т-\;F_<с>=m\;\times\;a\) , где \(F_т\) — сила тяги, \(F_<с>\) — силы сопротивления.
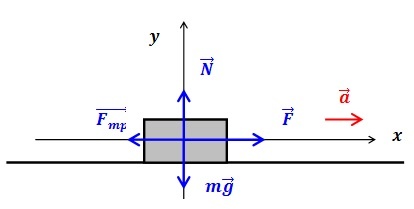
При решении конкретной задачи силы, воздействующие на тело, схематически изображают в виде векторов. На схеме:

сила тяжести mg;
сила реакции опоры \(N\) ;
сила трения \( F_<тр>\) ;
сила тяги \(F\) .

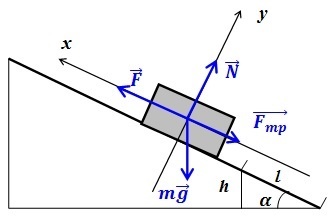
При нахождении тела на горизонтальной поверхности сила тяжести и сила реакции опоры уравновесят друг друга. Но если транспортное средство движется в гору или под гору, придется учесть влияние уклона. Тогда формула может выглядеть так: \(F_т-\;F_с-\;mg\;\times\;\sin\alpha=m\;\times\;a.\)

Работа A, которую должна совершить сила тяги, сдвигая тело, связана с ней соотношением \(A\;=\;F\;\times\;s\) . \(s\) здесь — расстояние, на которое тело переместилось.

Какое условие должно соблюдаться

Сила тяги всегда должна быть больше противодействующих ей сил.

Формула через мощность

Полезную механическую мощность \(N\) можно вычислить по формуле \(N=F_т\;\times\;v\) , где \(v\) — скорость. Для определения силы тяги нужно разделить мощность на скорость: \(F_т\;=\;\frac N v.\)

Измерение и обозначение силы тяги

Силу тяги обозначают \(F_т\) или \(F\) . Единица измерения — ньютон ( \(Н\) ).
Для решения задач недостаточно измерить усилие, приложенное к объекту, и выразить его конкретным числом, так как сила обладает еще и направлением. Чтобы подчеркнуть, что сила — векторная величина, к буквенному обозначению добавляют стрелку.

Как определить силу тяги двигателя. Примеры решения задач

Задача 1

Автомобиль может разгоняться до 216 км/ч. Максимальная мощность двигателя равна 96 кВт. Определите максимальную силу тяги двигателя.

Решение

Переведем киловатты в ватты, а километры в час — в метры в секунду:

\(F_т\;=\;\frac N v = \frac<96000> <60>= 1600 Н\)

Задача 2

Троллейбус весом 12 тонн за 5 секунд проезжает по горизонтальной дороге 10 метров. Сила трения равна 2,4 кН. Определите силу тяги, которую развивает двигатель.

Решение

Переведем тонны в килограммы, а килоньютоны в ньютоны:

\(F_т-\;F_<тр>=m\;\times\;a\) , следовательно, \(F_т=m\times a\;+\;F_<тр>\)

Чтобы определить ускорение а, воспользуемся формулой \(s\;=\;\frac2\)

Подставив численные значения величин, получаем:

Задача 3

Транспорт, весящий 4 тонны, едет в гору. Уклон — 1 метр на каждые 25 метров пути. \(\mu\) — 0,1 от силы тяжести, \(а = 0\) . Определите силу тяги.

Решение

Сделаем проекции на координатные оси:

Подставим значение \(F_<тр>\) в уравнение \(OX\) и определим \(F_т\) :

Найдем синус и косинус \(\alpha\) , подставим их в общую формулу:

Нужно подобрать материалы для студенческой работы?

Источник статьи: http://wiki.fenix.help/fizika/sila-tyagi

Зависимость силы тяги от скорости

Существует два режима движения локомотива, при которых сила тяги зависит от скорости различным образом. При движении со сравнительно небольшой скоростью, вплоть до так называемой критической скорости, запас мощности двигателей достаточен для создания предельной силы тяги. Сила тяги в этом режиме ограничена только потерей сцепления колеса с рельсом. Результаты экспериментальных измерений свидетельствуют о том, что предельная сила тяги сильно зависит от состояния материала, качества обработки и износа рельсов и колес, от погоды и еще большого числа факторов. Однако тенденция уменьшения предельной силы тяги с ростом скорости существует (рис. 3.3). Причиной этого может быть уменьшение времени процесса пластической деформации микробугорков в пятнах контакта при увеличении скорости движения. Поэтому число межмолекулярных связей между металлом колеса и рельса с ростом скорости тоже уменьшается, и это приводит к уменьшению силы тяги.

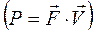
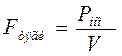
При движении со скоростью выше критической мощность двигателей достигает номинального значения и уже недостаточна для поддержания предельной силы тяги. По формуле мощности сила тяги уменьшается обратно пропорционально скорости:

. (3.3)

(Это похоже на уменьшение силы отталкивания бегуна от беговой дорожки по мере увеличения его скорости.)

Значение критической скорости V_кр можно определить, приравняв предельные значения силы тяги по сцеплению и по мощности (3.3) друг к другу

. (3.4)

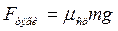
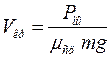
Нам важно ваше мнение! Был ли полезен опубликованный материал? Да | Нет

Источник статьи: http://studopedia.su/5_52789_zavisimost-sili-tyagi-ot-skorosti.html

Зависимость силы тяги от скорости

. (3.3)

(Это похоже на уменьшение силы отталкивания бегуна от беговой дорожки по мере увеличения его скорости.)

. (3.4)

Сила трения качения

При качении колеса по рельсу происходит деформация как колеса, так и рельса. Из-за остаточных деформаций уровень рельса за колесом оказывается ниже, чем перед колесом, поэтому колесо при движении должно все время закатываться на бугорок. Распределение давления на колесо со стороны рельса оказывается несимметричным: спереди давление больше, а сзади меньше (рис. 3.4). Точка приложения силы реакции рельса на колесо смещается вперед на небольшое расстояние b.

Разложим силу реакции на две компоненты. Нормальная составляющая реакции Q перпендикулярна площадке контакта и проходит через ось колеса, а касательная составляющая F_сц направлена почти вдоль рельса. Это сила сцепления. Она препятствует проскальзыванию колеса по рельсу. Разложим, в свою очередь, нормальную составляющую силы реакции Q на две компоненты: перпендикулярно рельсу N, и силу, направленную вдоль рельса, которая является силой трения качения F_кач.

Так как сила Q проходит через ось колеса, то сумма моментов сил ее составляющих относительно оси должна быть равна нулю: . Откуда получаем, что сила трения качения пропорциональна силе давления рельса на колесо:

. (3.5)

Здесь – коэффициент трения качения. Он уменьшается с ростом твердости материала рельса и колеса и с увеличением размеров колеса. Если бы за колесом при идеально упругих свойствах металла форма рельса восстанавливалась, то эпюра давления была бы симметричной, и трение качения отсутствовало бы.

Итак, в зоне контакта действуют две силы трения: диссипативная сила трения качения, направленная против скорости и консервативная сила сцепления, являющаяся силой трения покоя. При буксовании или юзе колеса сила сцепления превращается в диссипативную силу трения скольжения. На сопротивление при качении колеса влияет состояние железнодорожного полотна, удары о стыки рельсов, трение в подшипниках колесной пары, удары гребня бандажа о рельсы при извилистом движении колесной пары. Увеличивается сопротивления при движении на повороте, так как гребень переднего колеса упирается о наружный рельс. Вместе с силой трения качения все эти дополнительные воздействия создают общую силу сопротивления движению поезда. Будем считать, что суммарная сила сопротивления качению колес поезда подчиняется закону Кулона, то есть, пропорциональна силе нормального давления рельсов на колеса поезда. Так как сила нормального давления практически равна силе тяжести поезда, то закон для силы сопротивления качению примет вид

По экспериментальным измерениям, результирующий коэффициент сопротивления μ_сопр при качении стального колеса по рельсу, находится в пределах 0,003 – 0,008. Это много меньше, чем коэффициент трения скольжения. Поэтому катить легче, чем тащить. Столь малое значение коэффициента сопротивления обусловило эффективность и широкое распространение рельсового транспорта.

Сила торможения

Тормоз – это устройство на поездах, создающее искусственное сопротивление движению для уменьшения скорости. Для создания силы торможения при движении на колеса должен действовать момент сил торможения, создаваемый либо тормозными колодками, либо электромагнитными силами якорей тяговых двигателей при рекуперативном и реостатном торможении.

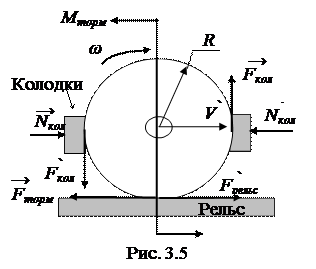
Силы трения скольжения между бандажом колеса и тормозными колодками создают момент сил, который противодействует вращению колеса при его качении. При стремлении колеса перестать вращаться, колесо толкает рельс вперед от себя с силой трения F_рельс (рис. 3.5). А рельс, согласно третьему закону Ньютона, толкает колесо назад с такой же по величине силой трения, которая является силой торможения F_торм. По своей природе это либо сила сцепления, если колесо не проскальзывает по рельсу, либо сила трения скольжения, если колесо проскальзывает. Движение юзом возникает при заклинивании колеса тормозными колодками.

На колесо действуют колодки и рельс. При торможении со сравнительно небольшим ускорением, момент сил со стороны тормозных колодок скомпенсирован моментом силы торможения со стороны рельса F_тормR = 2F_колR. Сила трения со стороны колодок, по закону трения скольжения, равна произведению коэффициента трения скольжения колодок μ_кол на силу давления двух тормозных колодок на бандаж N_кол,. Регулируя силу давления можно изменять величину силы торможения от нуля до предельного значения

Силы торможения не могут превышать предельного значения, которое будет на грани потери сцепления колеса с рельсом

где ΔMg – часть силы тяжести вагона, приходящаяся на одно колесо, μ_сц –коэффициент сцепления колеса и рельса.

При слишком большой силе нажатия тормозных колодок на бандаж колеса или при возрастании коэффициента трения скольжения колодки (так бывает для чугунных колодок при уменьшении скорости поезда), колесо может заклинить. Колесо, не вращаясь, скользит по рельсу, движется юзом. Это приводит к негативным последствиям. Происходит износ рельса, на колесе образуется лыска (ползун) и оно теряет круглую форму, увеличивается тормозной путь поезда так как сила трения скольжения меньше силы сцепления. Для предотвращения юза колесо следует на короткое время отпустить и затем вновь прижать колодки с меньшим усилием.

Задачи

1. Определить момент сил, развиваемый тяговым электродвигателем, при котором ведущее колесо начнет буксовать? Коэффициент сцепления колеса с рельсом 0,20, радиус колеса 0,59 м, передаточное отношение редуктора 4,2. Сцепной вес, приходящийся на колесо, 200 кН.

2. Определить наименьший уклон рельсов, при котором вагон массой 50 т покатится. Коэффициент сопротивления качению колес 0,002.

3. Мощность тяговых двигателей локомотива 3,0 МВт. Какую силу тяги развивает локомотив массой 200 т при скорости 15 м/с? Определите, будет ли буксование колес, если коэффициент сцепления 0,25?

4. Определить, критическую скорость движения локомотива массой 200 т с тяговыми двигателями мощностью 4 МВт, чтобы не наступило буксование колес по рельсам. Коэффициент сцепления 0,25.

5. Определить силу торможения, достаточную для равномерного движения поезда массой 2000 т на спуске с уклоном 0,010. Коэффициент сопротивления качению колес 0,004. Определить максимальный уклон, при котором начнется скольжение поезда юзом, если коэффициент сцепления колес с рельсами 0,20.

6. При каком значении силы давления на тормозные колодки колесо четырехосного вагона массой 50 т начнет скользить по рельсу, двигаться юзом. Коэффициент трения скольжения колеса по рельсам 0,25, коэффициент трения скольжения колодки по колесу 0,15.

7. Поезд массой 800 т спускается в карьер с постоянной скоростью в режиме торможения, и поднимается груженым с общей массой 3000 т также равномерно. Определить, когда и во сколько раз угон рельсов больше, считая, что он пропорционален касательной силе воздействия колес на рельсы. Коэффициент трения качения колес 0,005.

4. ДИНАМИКА ПОСТУПАТЕЛЬНОГО ДВИЖЕНИЯ

Движение тел при воздействии на них других тел изучает динамика. Динамика основана на трех законах Ньютона, сформулированных в фундаментальном труде «Начала натуральной философии» в 1687 г.

Законы Ньютона

Первый закон Ньютона

Всякое тело находится в состоянии покоя или равномерного и прямолинейного движения до тех пор, пока воздействие со стороны других тел не заставит изменить это состояние.

Свойство тел сохранять состояние покоя или равномерного прямолинейного движения называется инерцией. Первый закон Ньютона называют законом инерции, а системы отсчета, в которых справедлив закон инерции – инерциальными системами отсчета (ИСО). Всякая система отсчета, движущаяся по отношению к ИСО поступательно, равномерно и прямолинейно также является ИСО. Во всех равноправных ИСО законы физики одинаковы.

Тел, на которые ничто не действует, нет. Однако можно добиться того, чтобы воздействия со стороны других тел были бы скомпенсированы, и тогда первый закон динамики будет выполнен. И наоборот, выполнение первого закона динамики позволяет обнаруживать инерциальные системы отсчета и только тогда можно применять второй и третий законы Ньютона.

Например, в вагоне при движении на повороте или при резком торможении без всякого видимого внешнего воздействия тела относительно вагона начинают перемещаться. Следовательно, вагон или другие тела, движущийся ускоренно, не являются инерциальными системами отсчета. В то же время для наблюдателя на платформе движение тел внутри вагона происходит по инерции. То есть платформа и Земля являются инерциальными системами отсчета. (На самом деле Земля вращается, но её центростремительное ускорение сравнительно невелико и Землю для транспортных средств можно считать инерциальной системой отсчета).

Второй закон Ньютона

Это основной закон динамики поступательного движения. Ускорение тела прямо пропорционально силе F, действующей на тело, обратно пропорционально массе и направлено по линии действия силы:

. (4.1)

Масса тела, согласно закону, является мерой инертности тела при поступательном движении. Массу тел определяют сравнением с массой эталона в 1 кг, который служит единицей массы. Известно, что масса тела входит в закон всемирного тяготения. Различие между гравитационной и инертной массами с точностью до погрешности опыта не обнаружено. Это позволяет определять массу тел взвешиванием.

Сила является характеристикой взаимодействия тел. Воздействие силы приводит к изменению движения тела, то есть к ускорению и к деформации тел. Поэтому при известной массе тела по его ускорению на основании второго закона Ньютона можно количественно определить величину силы и ее направление. Величину силы также можно определить по деформации пружины динамометра, согласно закону Гука F = – kx. В системе СИ единицей силы является ньютон (Н). Это сила, сообщающая телу массой в 1 кг ускорение 1 м/с 2 .

Перепишем уравнение второго закона Ньютона (4.1) в другом виде, подставив ускорение как первую производную от скорости по времени

. (4.2)

Векторная величина, равная произведению массы тела на вектор его скорости , называется импульсом тела, а произведение вектора силы на время её действия – импульсом силы. Тогда формулировка второго закона динамики, данная самим Ньютоном, примет вид: изменение импульса тела равно импульсу приложенной к телу силы и происходит в направлении действия силы.

Если на тело действует несколько сил, то результирующее ускорение определяется результирующей силой, которая равна векторной сумме, всех сил.

Третий закон Ньютона

Силы взаимодействия тел равны по величине и противоположны по направлению:

(4.3)

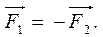
Если одна из сил есть действие, то вторая – противодействие. Поэтому действию всегда есть равное и противоположное противодействие. Силы всегда возникают попарно и они приложены к разным телам, поэтому никогда не уравновешивают друг друга. Силы имеют одинаковую природу.

Источник статьи: http://lektsii.org/6-70017.html